
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример решения задачи 3.3
Пусть: m1 =100, m2 = 150, m3 = 400 кг, М=4200+200t Нм, МС =2000 Нм = соnst,
R1=60, R2=40 cм, r2=20 cм, ix1=20√2, ixb= 30см, w10= 2c-1.
Найти уравнение 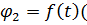 вращательного движения звена второго механизма), а также окружное усилие S в точке касания звеньев 1 и 2 и натяжение нити Т в момент времени t1 (рис.3.6).
вращательного движения звена второго механизма), а также окружное усилие S в точке касания звеньев 1 и 2 и натяжение нити Т в момент времени t1 (рис.3.6).
Решение
К звену 1 механизма приложена сила тяжести 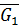 , движущий момент М, составляющие реакции подшипника
, движущий момент М, составляющие реакции подшипника  ,
, 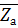 , окружное усилие
, окружное усилие 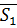 и нормальная реакция
и нормальная реакция  звена 2.
звена 2.
К звену 2 механизма приложена сила тяжести 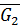 , момент сил сопротивления
, момент сил сопротивления 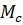 , составляющие реакции подшипника
, составляющие реакции подшипника 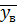 ,
,  , натяжение нити Т, к которой подвешен груз 3, окружное усилие
, натяжение нити Т, к которой подвешен груз 3, окружное усилие  и нормальная реакция
и нормальная реакция 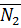 звена 1.
звена 1.
К грузу 3 приложена сила тяжести 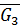 , и натяжение нити Т.
, и натяжение нити Т.

Рисунок 3.6.
Очевидно:  = -
= - 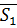 ,
,  = -
= - 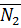 и
и 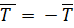 .
.
Составим дифференциальное уравнение вращения звена 1 вокруг неподвижной оси 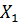 :
:
 =
=  .
.
Главный момент  внешних сил, приложенных к звену 1 относительно оси
внешних сил, приложенных к звену 1 относительно оси 
Момент М приводит в движение систему и поэтому принят положительным, а момент, создаваемый усилием  , препятствует вращению звена 1 и, следовательно, отрицателен.
, препятствует вращению звена 1 и, следовательно, отрицателен.
Дифференциальное уравнение вращательного движения звена 1 примет вид 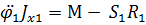 .
.
Выразим угловое ускорение 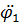 звена 1 через угловое ускорение
звена 1 через угловое ускорение  звена 2.
звена 2.
Так как  , то
, то 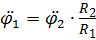 .
.
Тогда уравнение принимает следующий вид: 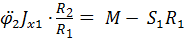
Для составления дифференциального уравнения вращения вокруг оси  звена 2, к которому подвешен груз 3, применим теорему об изменении кинетического момента
звена 2, к которому подвешен груз 3, применим теорему об изменении кинетического момента

Кинетический момент системы 2-3 относительно оси 
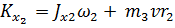 ,
,
где 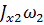 - кинетический момент звена 2, вращающегося с угловой скоростью
- кинетический момент звена 2, вращающегося с угловой скоростью 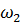 вокруг неподвижной оси
вокруг неподвижной оси  ;
;
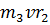 - момент количества движения груза 3, движущегося поступательно со скоростью V. Так как V=
- момент количества движения груза 3, движущегося поступательно со скоростью V. Так как V= 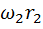 ,
,
 ,
,
где 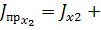
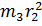 - приведённый к оси
- приведённый к оси  момент инерции системы 2-3.
момент инерции системы 2-3.
Главный момент 
Момент, создаваемый усилием  , приводит к движению системы 2-3 и поэтому принят положительным, а момент силы тяжести груза
, приводит к движению системы 2-3 и поэтому принят положительным, а момент силы тяжести груза 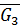 и момент сил сопротивления
и момент сил сопротивления 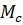 препятствует движению системы и, следовательно, отрицательны.
препятствует движению системы и, следовательно, отрицательны.
Таким образом, получаем
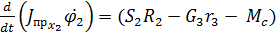
Дифференциальное уравнение вращения звена 2:
 =
=  .
.
В полученной системе уравнений

Неизвестные усилия  и угловое ускорение
и угловое ускорение  . Исключим
. Исключим  , для чего первое уравнение этой системы умножим на
, для чего первое уравнение этой системы умножим на 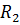 , второе на
, второе на 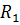 и сложим соответствующие части уравнений:
и сложим соответствующие части уравнений:
( )
) 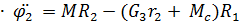 ,
,
Отсюда 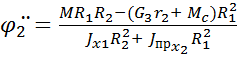 .
.
Данное выражение определяет в общем виде угловое ускорение звена 2 механизма.
Учитывая исходные данные, найдём:
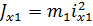 = 100
= 100  (0,2
(0,2  )2 = 8 кг м2,
)2 = 8 кг м2,
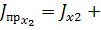
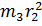 =
= 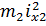 +
+ 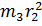 = 150·0,32 + 400·0,22 =29,5 кг м2
= 150·0,32 + 400·0,22 =29,5 кг м2
тогда 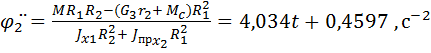
Интегрируем это выражение дважды:
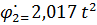 + 0,4597t +
+ 0,4597t + 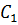 ;
; 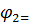 0,672 t3 + 0,230 t2 + C1t + C2
0,672 t3 + 0,230 t2 + C1t + C2
Для определения постоянных интегрирования используем начальные условия задачи: при t = 0; 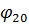 = 0;
= 0;
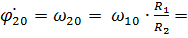 2 ·
2 · 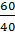 = 3
= 3 
Следовательно,  = С1;
= С1; 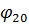 = С2, т.е. С1 = 3 с-1, С2 = 0.
= С2, т.е. С1 = 3 с-1, С2 = 0.
Уравнение угловой скорости звена 2 имеет вид

 2,017·t2 + 0, 4597·t + 3, с-1.
2,017·t2 + 0, 4597·t + 3, с-1.
Искомое уравнение вращательного движения звена 2 имеет вид
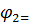 0,672·t3 + 0,230·t2 + 3t, рад.
0,672·t3 + 0,230·t2 + 3t, рад.
Окружное усилие S можно определить из уравнения:
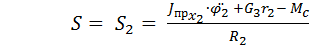 , при t = 1 c
, при t = 1 c
| Рис. 3.7. |

= 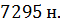
| Рис.11.5 |
 =
=  , из которого T=
, из которого T= 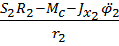 ,
,
при t = 1 c
| Рис. 11.5. |
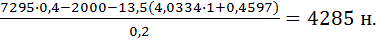
Задача 3.4.
Данная задача решается с применением теоремы об изменении кинетической энергии механической системы. Прежде всего, требуется определить систему, т.е. перечислить те тела, которые включены в состав системы. Затем нужно изобразить систему в произвольный момент времени, показать все силы (заданные и реакции связей), действующие на тела системы, определить скорости тел и перемещения точек приложения сил. После этого необходимо вычислить кинетическую энергию системы в начальном и конечном положениях, вычислить работу всех сил на заданных перемещениях и подставить полученные результаты в формулу, выражающую теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме. Исходные данные приведены в табл. 3.4., а схемы- на рис. 3.8.
|
|
Дата добавления: 2014-11-25; Просмотров: 423; Нарушение авторских прав?; Мы поможем в написании вашей работы!