Пример решения задачи 3.1

Условие. Груз весом Р движется вниз по шероховатой наклонной плоскости, составляющей угол a=30°с горизонтом. Коэффициент трения скольжения груза о плоскость f=0,16. В начальный момент груз находился в положении М_о на расстоянии a=9 м от начала координат и имел скорость v₀=30 м/с. Определить уравнение движения груза в заданной системе координат (рис. 3.2).

Рис. 3.2

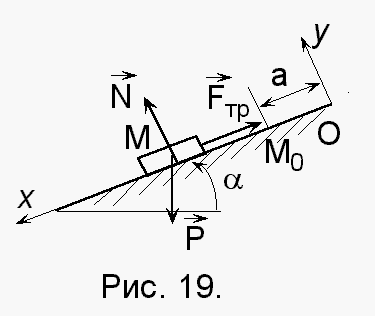Решение. 1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (шероховатой наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения F_тр. Тогда тело будет двигаться под действием системы трех сил (Р, N, F_тр).

1. Примем тело за материальную точку. Проектируя основное уравнение динамики точки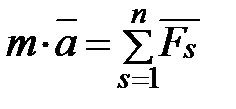

на оси декартовых координат Оx и Оy (ось Оx совпадает с направлением движения точки), получим два дифференциальных уравнения:

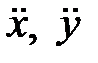Здесь m – масса точки; – проекции ускорения точки на соответствующие оси.

Так как тело движется прямолинейно вдоль оси Оx, то проекция ускорения на ось Оy равна нулю, следовательно, уравнение (3.2) примет вид .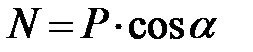

Сила трения по закону Кулона равна 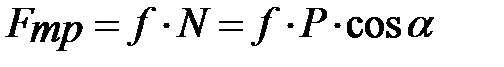. С учетом этого выражения дифференциальное уравнение (3.1) примет следующий вид:

.

После замены , где – ускорение свободного падения тела, и очевидных преобразований получим следующее дифференциальное уравнение второго порядка:

.

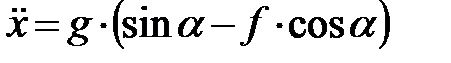Для понижения порядка уравнения произведем замену , получим дифференциальное уравнение первого порядка с разделяющимися переменными:

.

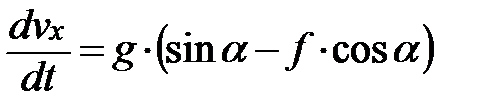Разделив переменные, проинтегрируем дифференциальное уравнение с учетом начальных условий (при t=0, v_x=v₀):

Произведем замену для понижения порядка уравнения 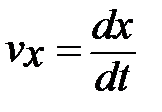и, разделив переменные, проинтегрируем дифференциальное уравнение второй раз с учетом начальных условий (при t=0 x=x₀=a):

Подставив в соотношение (4.4) значения заданных величин, получим окончательно следующее уравнение движения груза:

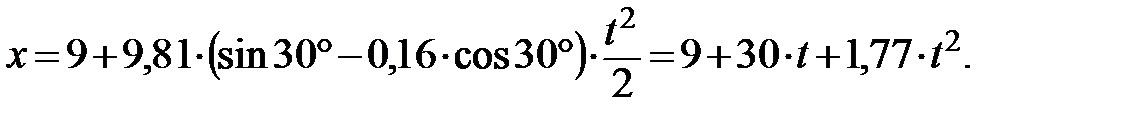
Задача 3.2

Данная задача на определение скорости материальной точки решается с применением теоремы об изменении количества движения.

Телу массой m сообщена начальная скорость v₀, направленная вверх по наклонной плоскости, составляющей угол α с горизонтом. На тело действует сила P, направленная в те же сторону (рис. 3.3).

Рис.3.3

Зная закон изменения силы Р=Р(t) и коэффициент трения скольжения f, определить скорость тела в момент времени t₁ , t₂, t₃ и проверить полученный результат для момента времени t₁ с помощью дифференциального уравнения движения.

Необходимые для решения данные приведены в таблице 3.2

Таблица 3.2.

Цифра шифра	1-я цифра шифра	2-я цифра шифра	3-я цифра шифра
m, кг	v0, м/с	t1, с	t2, с	t3, с	P0, Н	P1, Н	P2, Н	P3, Н	α, град	f
		5,4									0,10
		3,0									0,25
		4,0									0,10
		4,5									0,12
		9,0									0,08
		4,0									0,06
		8,0									0,20
		7,6									0,12
		5,0									0,20
		12,0									0,08

При построении графика изменения силы Р по заданным её значениям Р₀, Р₁, Р₂, Р₃ для момента времени t₀, t₁ , t₂, t₃, считать зависимость Р=Р(t) между указанными моментами времени линейной. Значение силы Р, задаваемое по табл. 3.2 в виде дроби, указывает на то, что модуль силы в заданный момент времени претерпевает «скачок»: в числителе указан модуль силы в конце промежутка времени, а в знаменателе – в начале следующего промежутка времени.

Дата добавления: 2014-11-25