Непрерывность и точки разрыва функции

Замечательные пределы

Нахождение пределов функции.

Следующие теоремы обеспечивают нахождение пределов функций. Пусть пределы 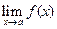и 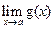существуют. Тогда:

1. ;

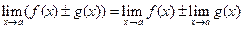2 ;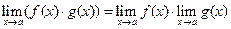

3. 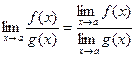(при ).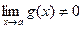

Также используются следствия:

1. ;

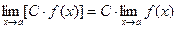2. .

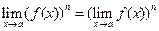Вычисление пределов следует начинать с подстановки вместо 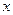его предельного значения в выражение для функции 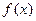, стоящей под знаком предела. При этом может получиться, что выражение 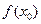не имеет смысла. Например, получается одно из выражений вида 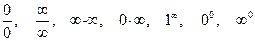. Но это не означает, что функция не имеет предела, говорят, что имеет место неопределенность.

Для раскрытия неопределенности над функцией 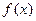проводят преобразования. Также используют первый замечательный предел 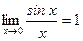, и второй замечательный предел .

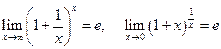Рассмотрим примеры нахождения пределов функций.

1. .

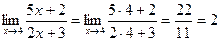2. .

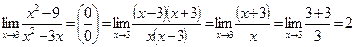3.

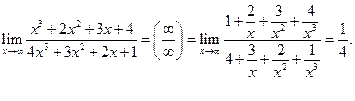
4. .

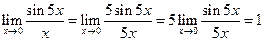5.

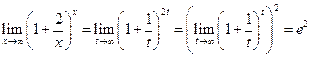
Представление о непрерывности функции интуитивно связано у нас с тем, что её графиком является плавная, нигде не прерывающаяся линия. Строгое определение непрерывности функции в точке следующее.

Функция называется непрерывной в точке , если она удовлетворяет трем условиям: 1. Функция определена в точке и в некоторой её окрестности, то есть существует 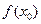; 2. Имеет конечный предел при 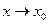, то есть 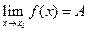; 3. Этот предел равен значению функции в точке , то есть .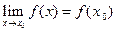

Например, все три условия для функции 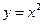в точке 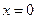выполнены, и она является непрерывной в этой точке. Для функции 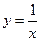в точке 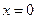первое условие не выполнено и она не является непрерывной в этой точке. Функция 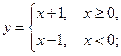не имеет общего предела в точке 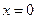, то есть не выполняется второе условие и непрерывность нарушается в этой точке. Для функции 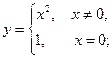не выполняется третье условие в точке 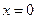, и она не является непрерывной в этой точке.

Функция называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если существуют пределы 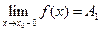и 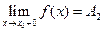, то точка называется точкой разрыва первого рода. В случае, когда 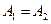, – точка устранимого разрыва. Если один из этих пределов не существует или равен 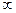, то точка называется точкой разрыва второго рода. Например, величина налоговой ставки 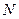от дохода 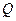имеет график.

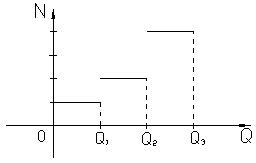
На концах промежутков эта функция имеет точки разрыва, причем они являются точками разрыва первого рода.

Отметим некоторые свойства функций непрерывных на отрезке. Функция, непрерывная на отрезке, хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.Если функция непрерывна на отрезке, то она ограничена на этом отрезке. Пусть функция непрерывна на отрезке и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка найдется, по крайней мере, одна точка, в которой функция обращается в ноль.

Дата добавления: 2014-11-26