Раскрытие неопределенностей по правилу Лопиталя

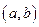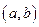Основой этого правила является следующая теорема Коши. Если функции , непрерывны на отрезке и дифференцируемы на интервале причем , то на интервале найдется хотя бы одна такая точка 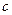, такая, что

.

Правило Лопиталя следующее. Предел отношения двух дифференцируемых функци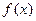и и в случае неопределенности вида или равен пределу отношения их производных, если последний существует, то есть

, .

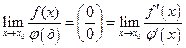Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Заметим, что если отношение производных опять представляет собой неопределенность вида или то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Рассмотрим примеры раскрытия неопределенностей по правилу Лопиталя.

1.

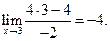
2. .

3.

=

Приведем пример, когда предел нельзя вычислить, используя, привило Лопиталя

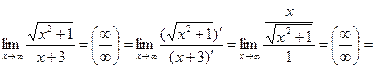
Для вычисления предела нужно числитель и знаменатель дроби разделить на переменную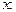

Дата добавления: 2014-11-26