Экстремума функции

Необходимое и достаточное условие

Точка называется точкой максимума функции , если в некоторой окрестности точки выполняется неравенство , и точкой минимума, если 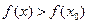. Значения функции в этих точках называют соответственно максимумом и минимумом функции. Максимум и минимум функции объединяют общим названием экстремум функции.

Экстремум функции часто называется локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с достаточно малой окрестностью точки. Может оказаться, что на одном промежутке функция может иметь несколько экстремумов, причем минимум в одной точке может быть больше максимума в другой точке.

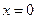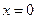Если в точке дифференцируемая функция имеет экстремум, то касательная в этой точке параллельна оси абсцисс и выполняется условие теоремы Ферма . Функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, функция имеет минимум в точке , не дифференцируема в этой точке. Функция также имеет в точке минимум, а производная в этой точке 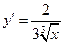не существует. Таким образом, из приведенных примеров следует следующее необходимое условие экстремума.

Для того чтобы функция имела экстремум в точке , необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Точки, в которых выполнено необходимое условие экстремума, называются критическими или стационарными точками. Критические точки должны входить в область определения функции.

Может оказаться, что критическая точка не является точкой экстремума. Например, функция 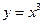возрастает на всей числовой прямой, так как . В точке 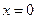производная рана нулю, но экстремума в этой точке нет. Функция также возрастает на всей числовой прямой, так как . В точке производная не существует, а экстремума в этой точке нет. Таким образом, для нахождения точек экстремумов функции требуется дополнительное исследование критических точек, т.е. требуется достаточное условие экстремума функции. Эти достаточные условия определяют следующие теоремы.

Теорема 1. Если при переходе через критическую точку производная дифференцируемой функции меняет свой знак с плюса на минус, то точка есть точка максимума функции , а если с минуса на плюс, – то точка минимума этой функции.

Теорема 2. Второе достаточное условие экстремума. Если первая производная дважды дифференцируемой функции равна нулю в точке , а вторая производная в этой точке больше нуля , то точка есть точка минимума функции , если вторая производная меньше нуля , то – точка максимума функции.

Схема исследования функции на экстремум следующая. 1. Найти область определения функции . 2. Найти первую производную функции и определить критические точки функции, в которых производная 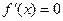или не существует. 3. Определить знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции. 4. Вычислить значение функции в точках экстремума.

Например, исследовать на экстремум функцию 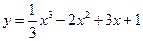. Имеем: 1. Область определения функции – все действительные числа. 2. Находим первую производную 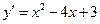и определяем критические точки из условия : , 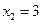. 3. Отмечаем эти точки на числовой прямой и определяем знак производной на каждом из полученных промежутков, делаем вывод о наличии экстремума.

4. Вычисляем значения функции в точке максимума и минимума 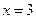. Получаем , .

Теория нахождения экстремумов функции применяется при решении различных экономических задач, в которых нужно найти максимум или минимум какой-то величины, заданной функциональной зависимостью.

Например, функция прибыли при объеме выпускаемой продукции 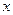имеет вид . Найти оптимальный объем выпуска продукции и прибыль. Функция прибыли определена для значений , , 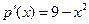, с учетом того, что , критическая точка 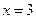. Найдем вторую производную функции прибыли и ее значение в критической точке. Имеем: , . Следовательно, по второму достаточному условию экстремума функция прибыли имеет максимум для объема выпускаемой продукции 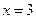. Прибыль будет следующей: единиц измерения.

Дата добавления: 2014-11-26