Формула Тейлора

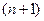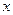Если функция имеет в точке и в некоторой ее окрестности производные до порядка включительно, то есть , то для любой точки этой окрестности между точками и 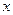найдется точка 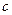такая, что имеет место следующая формула Тейлора

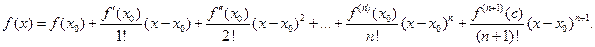
Последнее слагаемое называется остаточным членом формулы Тейлора. Здесь .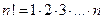

По этой формуле любую дифференцируемую необходимое количество раз функцию можно с большой точностью заменить целой рациональной функцией – многочленом Тейлора.

Если в формуле Тейлора 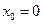, то из нее получаем формулу Маклорена

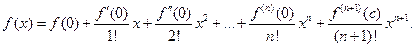
Для функций , , 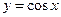имеем соответственно разложение по формуле Маклорена:

,

,

.

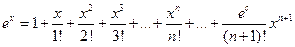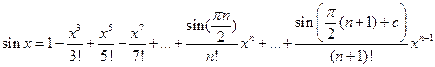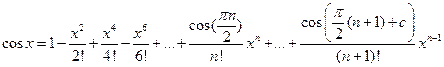Используя эти формулы, можем вычислить значения этих функций для данного значения 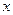с необходимой точностью.

Например, при x =1, ограничиваясь n =8, получим формулу, позволяющую найти приближенное значение числа :

.

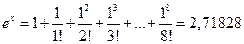Дата добавления: 2014-11-26