Функциональные и степенные ряды

Признак сходимости знакочередующихся рядов

Числовой ряд 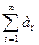называется знакочередующимся, если члены ряда и 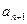для любых 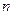имеют разные знаки. Знакочередующийся ряд записывают в виде , где 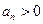. Признак сходимости для знакочередующихся рядов следующий.

Признак Лейбница. Если абсолютные величины членов знакочередующегося ряда

монотонно убывают: и общий член ряда стремится к нулю , то ряд сходится.

Например, ряд 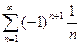условно сходится, так как удовлетворяет условиям признака Лейбница:

1) 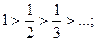2) ,

а ряд 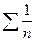, составленный из абсолютных величин его членов, расходится, так как он гармонический ряд.

Признак Лейбница сходимости знакочередующегося ряда иногда называют признаком условной сходимости.

Выражение 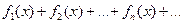называется функциональным рядом. Слагаемыми в таком ряду являются функции. Если переменной 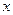дать конкретное числовое значение , то получим числовой ряд из значений функций в точке : .

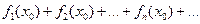Точка называется точкой сходимости функционального ряда, если числовой ряд 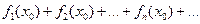сходится. Множество всех точек сходимости функционального ряда называется областью сходимости.

Практическое применение имеют степенные ряды, то есть ряды, слагаемыми которых являются степенные функции с натуральными показателями. Степенной ряд записывают в виде

,

где числа 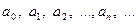называются коэффициентами степенного ряда.

Придавая 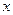различные значения в этом ряде, будем получать различные числовые ряды, которые могут быть сходящимися или расходящимися.

Если 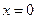, то ряд 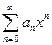принимает вид 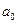, то есть его сумма равна 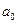. Итак, степенной ряд имеет, по крайней мере, одну точку сходимости – начало координат. Ответ на вопрос об области сходимости степенного ряда дает теорема Абеля.

Теорема. Если ряд 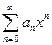сходится при 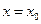, то он абсолютно сходится при всех значениях 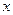, удовлетворяющих неравенству 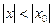, если же ряд 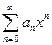расходится при 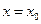, то он расходится при всех значениях 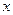, удовлетворяющих неравенству .

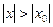Например, степенной ряд 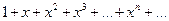составлен из членов геометрической прогрессии со знаменателем . Этот ряд сходится, если . Отсюда , то есть областью сходимости является интервал . Ряд расходится для значений .

Дата добавления: 2014-11-26