Переменного

Комплексные числа. Функция комплексного

Лекция 17. Гармонический анализ

Комплексным числом называется упорядоченная пара z= (x,y) вещественных чисел, первое из которых х называется действительной частью, а второе у – мнимой частью. Пишут Rez=x, Imz=y.

Суммой чисел z₁= (x₁,y₁) и z₂= (x₂,y₂) называется число z=(x₁+x₂, y₁+y₂).

Произведением этих чисел называется число z=(x₁x₂-y₁y₂; x₁y₂+x₂y₁).

Разностью этих чисел называется число z=(x₁-x₂, y₁-y₂).

Частным чисел z₁= (x₁,y₁) и z₂= (x₂,y₂)¹0 называется такое комплексное число z, которое при умножении на z₂ дает z₁:

В операциях с комплексными числами особую роль играет число (0,1)= i – мнимая единица:

.

Комплексное число z= (x,y) можно представить через мнимую единицу так:

z=x+iy.

Такое представление позволяет производить операции с комплексными числами как с алгебраическими многочленами.

Комплексное число можно изобразить точкой плоскости (рис. 1).

Рис. 1. Изображение комплексного числа на плоскости

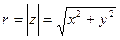– модуль комплексного числа, r – это расстояние точки z от начала координат.

Угол, образованный радиус-вектором точки z с осью ОХ, называется аргументом этой точки

.

Наименьшее по модулю значение 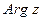называется главным значением его и обозначается arg z

.

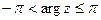Для аргумента j имеем .

Комплексное число можно записать в тригонометрической форме:

.

Сложение и вычитание комплексных чисел в тригонометрической форме производится так же, как и в алгебраической форме.

Умножение, деление, возведение в степень и извлечение корня в тригонометрической форме производятся по следующим формулам:

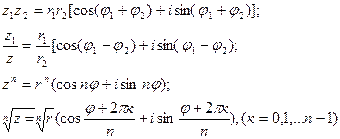
Введем понятие функции комплексного переменного.

Пусть даны две плоскости комплексных чисел z=x+iy и w=u+iv. Рассмотрим множество точек D в плоскости z и множество G в плоскости w.

Если каждому числу zÎD по некоторому закону поставлено в соответствие определенное комплексное число w ÎG, то говорят, что на множестве D задана однозначная функция комплексного переменного, отображающая множество D в множество G. Обозначение w=f (z).

Множество D называется областью определения функции f (z), G - область значений функции. Функцию f (z) можно записать в виде

,

где 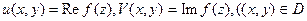– действительные функции от переменных х,у.

Говорят, что функция w=f (z)= u (x,y)+ iv (x,y) имеет предел в точке z₀, равный числу А=а+ib, если .

В этом случае пишут .

Функция w=f(z) = u (x,y)+ iv (x,y) называется непрерывной в точке z₀, если она определена в окрестности точки z₀ и для нее выполняется свойство:

.

Производной от функции f(z) в точке z называется предел

.

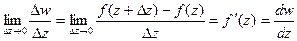Функцию f (z), имеющую непрерывную производную в любой точке области D комплексной плоскости, называют аналитической функцией на этой области.

Дата добавления: 2014-11-26