Траектория

Чтобы задать движение точки, надо задать ее в любом положении по отношению к выбранной системе отсчета в любой момент времени. Для задания движения точки можно применять один из следующих трех способов:

1. Естественный;

2. Координатный;

3. Векторный.

Естественный способ задания движения

Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория – прямая линия, то движение точки называется прямолинейным; а если кривая – то движение точки называется криволинейным.

Пусть кривая 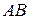является траекторией движения точки относительно системы отсчета 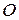, , 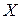, , 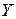(рис. 1.1.).

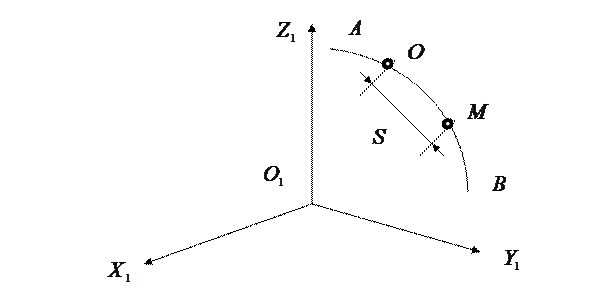
Рис. 7.1.

Выберем на этой траектории какую-нибудь неподвижную точку 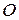, которую примем за начало отсчета; затем, рассматривая траекторию как криволинейную координатную ось, установим на ней положительное и отрицательное направление. Тогда положение точки будет однозначно определяться криволинейной координатой 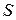, которая равна расстоянию от точки 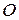до точки . Чтобы знать положение точки на траектории, в любой момент времени надо знать зависимость:

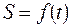(7.1.)

Уравнение (7.1.) выражает закон движения точки вдоль траектории. Таким образом, чтобы задать движения точки естественным способом, надо знать:

1. Траекторию точки;

2. Начало отсчета на траектории;

3. Законы движения точки вдоль траектории в виде .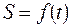

Координатный способ задания движения

Положение точки по отношению к данной системе отсчета , можно определить ее декартовыми координатами 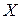, , 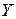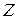(рис. 7.2.).

При движении все эти три координаты будут с течением времени изменяться. Чтобы знать закон движения точки, необходимо знать значения координаты точки для каждого момента времени, т.е. знать зависимости:

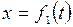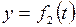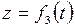; ; . (7.2)

Уравнения (7.2) представляют собой уравнения движения точки в декартовых координатах.

В случае плоского движения, например, точка движется в плоскости 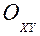, ее уравнения движения задаются в виде:

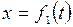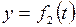, (7.3)

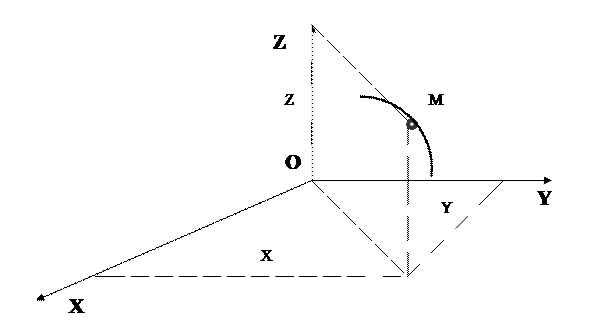
Рис. 7.2.

Уравнения (7.2), (7.3) представляют одновременно уравнения траектории точки в параметрической форме, где роль параметра играет величина 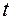. Исключив параметр 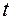, можно найти уравнение траектории в обычной форме, т.е. в виде, дающем зависимость между ее координатами:

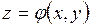– для пространственного движения;

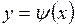– для плоского движения.

Векторный способ задания движения

Пусть точка движется по отношению к некоторой системе отсчета . Положение этой точки можно определить, задав вектор 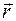, проведенный из начала координат 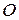в точку . Вектор 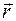называется радиусом – вектором точки . При движении точки вектор 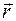будет с течением времени изменяться и по модулю и по направлению. Следовательно, 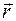можно задать вектором-функцией, зависящим от аргумента :

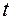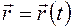(7.4.)

Геометрическое место концов вектора 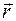, т.е. годограф этого вектора, определяет траекторию движущейся точки. Проектируя уравнение (7.4.) на оси координат получим:

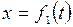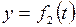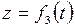; ; . (7.5).

Пример 1.

Заданы уравнения движения точки в координатной форме:

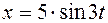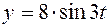; (плоское движение). Значения 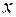и 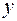в сантиметрах. Определить траекторию движения точки.

Решение.

Для определения траектории движения точки, необходимо исключить параметр 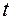из уравнений движения, заданных в координатной форме. Для этого возведем в квадрат данные уравнения:

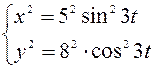, отсюда: .

Сложим соответственно левые и правые части полученных уравнений:

,

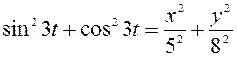Отсюда следует: 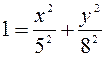, так как .

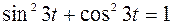Это есть каноническое уравнение эллипса с полуосями 5 и 8 см. Таким образом, данная точка совершает движение по эллипсу (рис.7.3.)

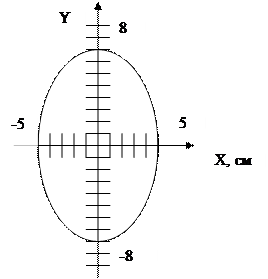Рис. 7.3.

Ответ: траектория движения точки – эллипс.

Пример 2.

Уравнения движения точки на плоскости задано:

, .

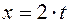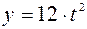Определить траекторию движения точки.

Решение.

Исключим параметр 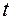из уравнений. Для этого из первого уравнения определим, что 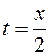и подставим во второе уравнение:

.

Таким образом, получим: .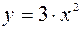

Графиком траектории движения точки является парабола (рис. 7.4.).

Рис. 7.4

Ответ: 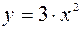– уравнение движения точки.

Пример 3.

Задано уравнение движения точки в векторной форме:

.

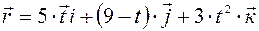Составить уравнение движения точки в координатной форме.

Решение.

Вследствие того, что 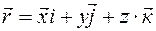, то отсюда следует:

; ;

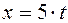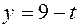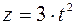
Ответ: уравнение движения точки: ; ; .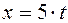

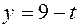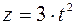Вопросы для самоконтроля

1. Что изучает кинематика?

2. Способы задания движения точки?

Задачи, рекомендуемые для самостоятельного решения: 10.1 – 10.23 [2].

Литература: [1], [3], [4].

Дата добавления: 2014-11-26