Касательное и нормальное ускорения точки

Касательное ускорение точки равно первой производной от модуля скорости или второй производной от расстояния по времени. Касательное ускорение обозначается – .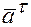

.

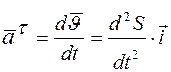Касательное ускорение в данной точке направлено по касательной к траектории движения точки; если движение ускоренное, то направление вектора касательного ускорения совпадает с направлением вектора скорости; если движение замедленное – то направление вектора касательного ускорения противоположно направлению вектора скорости. (рис. 8.5.)

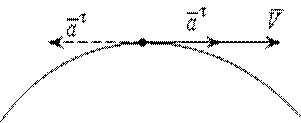
Рис. 8.5

Нормальным ускорением точки называется величина, равная квадрату скорости, деленному на радиус кривизны.

Вектор нормального ускорения направлен от данной точки к центру кривизны, (рис.8.6.). Нормальное ускорение обозначается .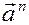

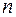– нормаль к данной точке на траектории движения.

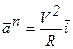
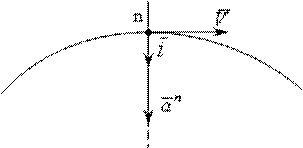
Рис. 8.6.

Полное ускорение точки 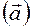определяется из векторного уравнения:

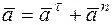
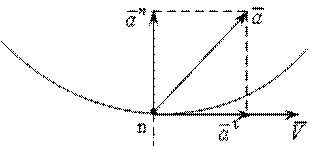
Рис. 8.7

Зная направление и модул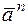и и 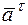, по правилу параллелограмма определим ускорение, соответствующее данной точке траектории движения. Тогда модуль ускорения 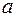определим:

.

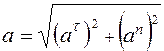Пример 1.

Определить траекторию, скорость и ускорение середины 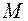шатуна кривошипно-шатунного механизма, если 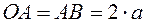, а угол 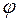при вращении кривошипа растет пропорционально времени: 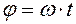(рис. 8.8.)

Рис. 8.8

Решение.

Определим уравнение движения точки 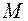. Для этого определим координаты точки 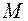в произвольном положении:

;

.

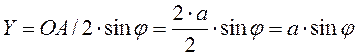Получим уравнения движения точки :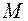

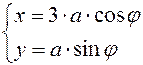или, учитывая, что : .

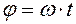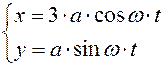Представим полученные уравнения в виде:

.

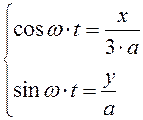Возводя эти равенства почленно в квадрат и складывая, получим:

.

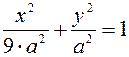Траектория точки 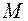представляет эллипс с полуосям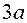и и .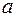

Определим проекции скорости точки 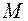на оси координат:

.

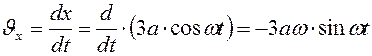
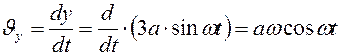Модуль скорости точки :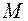

.

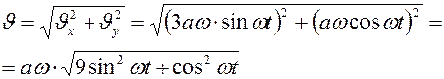Определим проекции ускорения точки 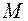на оси координат:

.

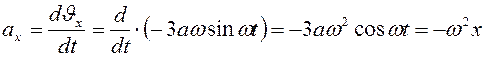
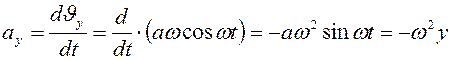Модуль ускорения определится как:

,

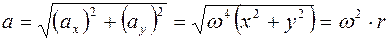где 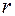– длина радиуса вектора, проведенного из начала координат в точку .

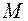Для определения направления ускорения точки 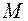найдем направляющие косинусы:

,

.

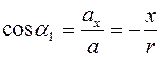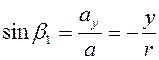Отсюда следует, что вектор ускорения 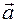все время направлен от точки 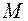к центру эллипса. (Рис. 8.8.)

Пример 2.

Даны уравнения движения точки: ; .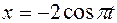

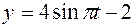Определить уравнение траектории точки для момента времени 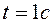. Найти положение точки, скорость и ускорение точки, а также ее касательное ускорение и радиус кривизны траектории в этой точке.

Решение.

1. Определим траекторию движения точки по уравнениям:

.

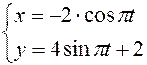Отсюда, возведя в квадрат обе части уравнений и складывая отдельно левые и правые части, получим:

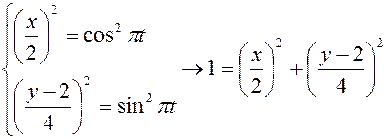
Траектория движения точки представляет эллипс с полуосями 2 и 4 с центром в точке с координатами (0,6) (рис. 8.9).

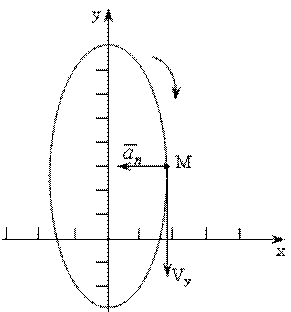
Рис. 8.9

2. В момент времени 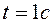точка находится в положении 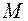с координатами: 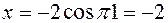; 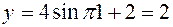, т.е. 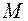(8.2).

Определим проекции скорости точки :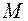

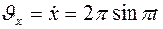
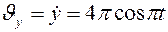
При 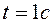получим:

; .

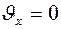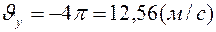Модуль скорости при 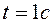будет:

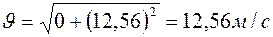
Отсюда следует, что точка движется по траектории по часовой стрелке. Вектор скорости направлен по касательной к траектории.

3. Определим проекции ускорения:

,

.

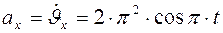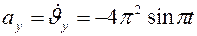При 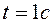проекции ускорений будут:

,

.

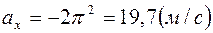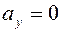Модуль ускорения:

,

.

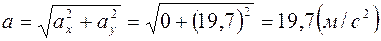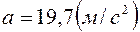Определим касательное ускорение точки при .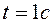

Так как ,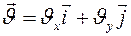

.

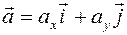Тогда .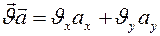

Вследствие того, что ,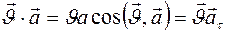

.

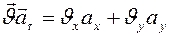Отсюда:

.

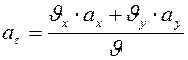Подставляя численные значения, получим:

.

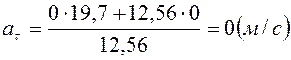Нормальное ускорение точки в данный момент времени:

,

.

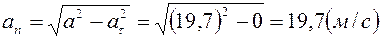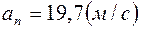Радиус кривизны в точке при 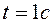будет:

,

.

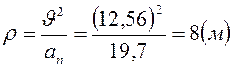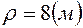Вопросы для самоконтроля

1. Определение скорости точки при различных способах задания движения?

2. Определение ускорения точки при различных способах задания движения?

Задачи, рекомендуемые для самостоятельного решения: 11.1 – 11.18, 12.1 – 12.39 [2].

Литература: [1], [3], [4].

Дата добавления: 2014-11-26