Тема 1. Cобытия. Вероятность событий

Пусть W={w} – конечное или счетное множество. Элементы множества W будем называть элементарными событиями, а само множество W – пространством элементарных событий.

Любое подмножество А множества W назовем событием. Обозначим через S класс событий, иначе S – класс подмножеств множества W.

Пусть каждому wÎW сопоставлено число Р(w) такое, что

.

Число Р(w) называется вероятностью элементарного события w.

Под вероятностью события А понимается число

.

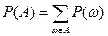Рассмотрим некоторою систему S событий А, В, С, …, каждое из которых может произойти, а может и не произойти. Между событиями системы S могут существовать известные отношения, с которыми мы постоянно будем сталкиваться.

1) Если каждый раз когда происходит событие А, происходит и событие В, то говорят, что А влечет за собой В, и обозначать: АÌВ или ВÉА.

2) Если А влечет за собой В и в то же время В влечет за собой А, то А и В равносильны: А=В.

3) Событие, состоящее в наступлении обоих событий А и В, называется произведением событий А и В: А∙В или АÇВ.

4) Событие, состоящее в наступлении хотя бы одного из событий А и В, называется суммой событий А и В: А+В или АÈВ.

5) Событие, состоящее в том, что событие А происходит, а событие В не происходит, называется разностью событий А и В: А–В или А\В.

6) Событие, состоящее в том, что событие А не происходит, называется противоположным для А:`А.

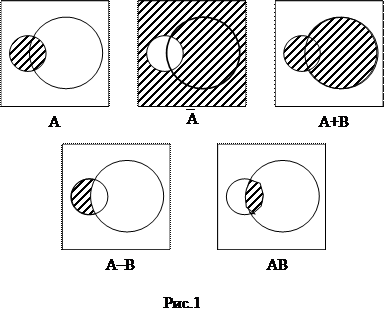Выберем наудачу внутри квадрата, изображенного на рисунке 1, точку. Обозначим через А событие «выбранная точка лежит внутри левого круга» и через событие В событие «выбранная точка лежит внутри правого круга». Тогда события А,`А, А+В, АВ, А–В состоят в попадании точки внутрь областей, заштрихованных на соответствующих фигурах рис.1.

7) Событие называется достоверным, если оно обязательно должно произойти в результате опыта. Например, при бросании двух игральных костей достоверно, что сумма очков будет не меньше двух.

Событие называется невозможным, если оно заведомо не может произойти. Например, при бросании двух игральных костей невозможно появление суммы очков, равной 13.

Очевидно, что все достоверные события равносильны между собой. Поэтому законно обозначать все достоверные события одной буквой – W. Все невозможные события тоже равносильны между собой. Любое невозможное событие будем обозначать знаком Æ.

8) Два события А и В называются несовместными, если их совместное появление невозможно, т.е., если АВ=Æ.

События В₁, В₂, …, В _п образуют полную группу событий, если хотя бы одно из них непременно должно произойти, т.е. если

В₁+В₂+…+ В _п =W.

Особенно существенны полные группы попарно несовместных событий.

9) В каждой задаче теории вероятностей приходится иметь дело с каким либо определенным комплексом условий и с какой-либо определенной системой S событий. Относительно этой системы целесообразно сделать следующие допущения:

a) если системе S принадлежат события А и В, то ей принадлежат также события АВ, А+В, А–В;

b) система S содержит достоверное и невозможное события.

Система событий, удовлетворяющая этим допущениям, называется полем событий.

Вероятность Р(А) можно рассматривать как функцию от события А, определенную на поле событий S. Эта функция обладает следующими свойствами:

1. Для достоверного события Р(W)=1.

2. Вероятность невозможного события равна нулю: Р(Æ)=0.

3. Для каждого А из S выполняется неравенство 0£Р(А)£1.

Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Тема 2. Классическое определение вероятности.

Рассмотрим пример. Пусть в ящике содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них – красные, 3 – синие и 1 – белый. Очевидно, возможность вынуть цветной (красный или синий) шар больше, чем возможность извлечь белый шар. Оказывается, что такую возможность можно охарактеризовать числом, которое называется вероятностью события (появления цветного шара).

Дадим этой возможности количественную характеристику. Пусть событие А – появление цветного шара. В нашем случае возможны шесть элементарных исходов: w₁ – появился белый шар; w₂, w₃ – появился красный шар; w₄, w₅, w₆ – появился синий шар. Эти исходы образуют полную группу попарно несовместных событий (обязательно появится только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и тщательно перемешаны).

Элементарные исходы, в которых наступает интересующее нас событие, назовем благоприятствующими этому событию. В нашем примере это 5 исходов: w₂, w₃, w₄, w₅, w₆.

Таким образом событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих А.

В рассматриваемом примере всего шесть элементарных исходов; из них пять благоприятствуют событию А. Вероятность того, что взятый шар окажется цветным, равна Р(А)=5/6. Это число дает количественную оценку степени возможности появления цветного шара.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

,

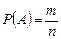где т – число элементарных исходов, благоприятствующих событию А; п – число всевозможных элементарных исходов испытания.

Здесь предполагается, что все элементарные исходы несовместны, равновозможны и образуют полную группу.

Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Дата добавления: 2014-11-26