Тема 8. Закон больших чисел

Математические законы теории вероятностей получены абстрагированием реальных статистических закономерностей, свойственных массовым случайным явлениям. Наличие этих закономерностей связано именно с массовостью явлений, т.е. с большим числом выполняемых однородных опытов или с большим числом складывающихся случайных воздействий, порождающих в своей совокупности случайную величину, подчиненную вполне определенному. Свойство устойчивости массовых случайных явлений известно человечеству еще с глубокой древности. В какой бы области оно ни проявлялось, суть его сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений; случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в массе взаимно погашаются, нивелируются, выравниваются. Именно эта устойчивость средних и представляет собой физическое содержание «закона больших чисел», понимаемого в широком смысле слова: при очень большом числе случайных явлений средний результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.

В узком смысле слова под «законом больших чисел» в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Закон больших чисел играет важную роль в практических применениях теории вероятностей. Свойство случайных величин при определенных условиях вести себя практически как не случайные позволяет уверенно оперировать с этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.

Возможности таких предсказаний в области массовых случайных явлений еще больше расширяются наличием группы предельных теорем, касающихся не предельных значений случайных величин, а предельных законов распределения. Речь идет о группе теорем, известных под название «центральной предельной теоремы». При суммировании достаточно большого числа случайных величин закон распределения суммы неограниченно приближается к нормальному при соблюдении некоторых условий. Эти условия, которые математически можно формулировать различным образом – в более или менее общем виде, – по существу сводятся к требованию, чтобы влияние на сумму отдельных слагаемых было равномерно малым, т.е. чтобы в состав суммы не входили члены, явно преобладающие над совокупностью остальных по своему влиянию на рассеивание суммы. Различные формы центральной предельной теоремы различаются между собой теми условиями, для которых устанавливается это предельное свойство суммы случайных величин.

Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли (имеются и другие теоремы, которые здесь не рассматриваются). Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим. Для доказательства этих теорем мы воспользуемся неравенством Чебышева.

Неравенство Чебышева. Вероятность того, что отклонение случайной величены Х от её математического ожидания по абсолютной величине меньше положительного числа e, не меньше, чем 1– :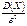

.

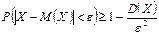Примечание. Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина Х выйдет за пределы участка 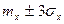, значительно меньше 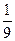. Например, для нормального закона эта вероятность приблизительно равна 0,003. Если закон распределения случайной величины неизвестен, а известны только т_х и s _х, на практике обычно считают отрезок 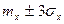участком практически возможных значений случайной величины (так называемое «правило трех сигма»).

Теорема Чебышева. Если Х₁, Х₂, …, Х _п, … – попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число e, вероятность неравенства

будет как угодно близка к единице, если число случайных величин достаточно велико.

Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонение каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.

В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало по сравнению со всей массой зерна, но само по себе оно достаточно велико.

Теорема Бернулли. Пусть m – число наступлений события А в п независимых испытаниях и р есть вероятность наступления события А в каждом из испытаний. Тогда, каково бы ни было e>0,

.

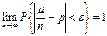Так как на практике часто неизвестные вероятности приходится приближенно определять из опыта, то для проверки согласия теоремы Бернулли с опытом было проведено большое число опытов. При этом рассматривались события, вероятности которых можно считать по тем или иным соображениям известными, относительно которых легко проводить испытания и обеспечить независимость испытаний, а также постоянства вероятностей в каждом из испытаний. Все подробные опыты дали прекрасное совпадение с теорией. Так например, французский естествоиспытатель XVIII века Бюффон бросил монету 4040 раз, герб выпал при этом 2048 раз. Частота появления герба в опыте Бюффона приближенно равна 0,507.

Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Дата добавления: 2014-11-26