Тема 4. Простейшие теоремы (сложения и умножения)

Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р(А+В)=Р(А)+Р(В).

Доказательство. Введем обозначения: п – общее число возможных элементарных исходов испытания; т ₁ – число исходов, благоприятствующих событию А; т ₂ – число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих событию А+В равно т ₁+ т ₂. Следовательно

,

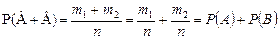что и требовалось доказать.

Следствие 1. Если события А₁, А₂, …, А _п образуют полную группу попарно несовместных событий, то сумма их вероятностей равна единице:

.

Следствие 2. Сумма вероятностей противоположных событий равна единице:

Р(`А)+Р(А)=1.

Теорема 2. Если события А и В совместны, то вероятность суммы этих событий выражается формулой:

Р(А+В)=Р(А)+Р(В)–Р(АВ).

Доказательство. Поскольку события А и В, по условию, совместны, то событие А+В наступит, если наступит одно из трех следующих несовместных событий: 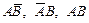. По теореме сложения вероятностей несовместных событий,

(*)

Событие А произойдет, если наступит одно из несовместных событий: 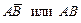. Поэтому

. (**)

Аналогично

. (***)

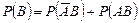Выразив из (**), (***) значения и подставив в (*), окончательно получим

Р(А+В)=Р(А)+Р(В)–Р(АВ),

что и доказывает теорему.

Следствие 1. Данный факт может быть обобщен на любое количество совместных событий:

,

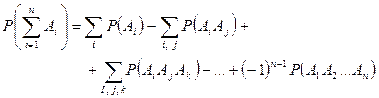где суммы распространяются на различные значения индексов i; i, j; i, j, k, и т.д.

Если никаких ограничений при вычислении вероятности Р(А) не налагается, то такие вероятности называются безусловными. Однако в ряде случаев приходится рассматривать вероятности событий при дополнительном условии, что произошло некоторое событие В. Такие вероятности мы будем называть условными и обозначать символом Р(А\В) или Р_В(А); это означает вероятность события А при условии, что событие В произошло.

Рассмотрим примеры.

1) Событие состоит в бросании двух монет; рассматриваются события:

А – появление герба на первой монете,

В – появление герба на второй монете.

В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А независимо от события В.

2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события;

А – появление белого шара у первого лица,

В – появление белого шара у второго лица.

Вероятность события А до того, как известно что-либо о событии В, равна 2/3. Если стало известно, что событие В произошло, то вероятность события А становится равной 1/2, из чего заключаем, что событие А зависит от события В.

Условие независимости событий А и В можно записать в виде: Р_В(А)=Р(А).

Теорема 3. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

Р(АВ)=Р(А) Р_А(В).

Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.

Следствие 2. Вероятность произведения независимых событий равна произведению вероятностей этих событий:

.

Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Дата добавления: 2014-11-26