Тема 7. Случайные величины, их законы распределения и числовые характеристики

Случайной величиной называется величина, которая в результате опыта может принять то илииное значение, неизвестно заранее – какое именно. Случайные величины подразделяются на два типа: дискретные (прерывные) и непрерывные. Возможные значения прерывных величин могут быть заранее перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.

Примеры дискретных случайных величин:

1) число появлений герба при трех бросаниях монеты (возможные значения 0, 1, 2, 3):

2) число отказавших элементов в приборе, состоящем из пяти элементов (возможные значения 0, 1, 2, 3, 4, 5):

3) число попаданий в самолет, достаточное для вывода его из строя (возможные значения 1, 2, 3, …, п, …).

Примеры непрерывных случайных величин:

1) абсцисса точки попадания при выстреле:

2) время безотказной работы радиолампы:

3) расстояние от точки попадания до центра мишени.

Случайные величины обозначаются большими латинскими буквами, а их возможные значения – соответствующими малыми буквами. Например, Х – число выпадений герба при двух бросаниях монеты; возможные значения: х ₁=0, х ₂=1, х ₃=2.

Для задания дискретной случайной величины необходимо перечислить все возможные ее значения и указать их вероятности.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Х	х 1	х 2	…	Хп
Р	р1	р3	…	Р п

Так как в одном испытании случайная величина принимает только одно возможное значение, то события Х= х ₁, Х= х ₂, …, Х= х_п образуют полную группу. Следовательно р₁+р₂+…+р _п =1. Если множество возможных значений Х бесконечно (счетно), то ряд р₁+р₂+…+р _п +… сходится и его сумма равна 1.

Для наглядности закон распределения дискретной случайной величины можно изобразить графически. В прямоугольной системе координат строят точки (х_i,р _i), затем их соединяют отрезками прямых. Полученную фигуру называют многоугольником распределения.

Для непрерывной случайной величины нельзя построить ряд распределения. Эта характеристика не является универсальной. Для количественной характеристики непрерывной случайной величины существует распределение вероятностей, в котором используют не вероятность события Х= х, а вероятность события Х< х, где х – некоторая текущая переменная. Эта функция называется функцией распределения случайной величины Х и обозначается F(х):

F(х)=Р(Х< х).

Функцию распределения F(х) иногда называют интегральной функцией распределения.

Свойства функции распределения.

1. Функция F(х) – неубывающая, т.е. при х ₁> х ₂ F(х₁) ³F(х₂).

2. F(–¥)=0.

3. F(+¥)=1.

Зная ряд распределения дискретной случайной величины, можно легко построить функцию распределения этой величины:

.

Когда текущая переменная х проходит через какое-нибудь из возможных значений прерывной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.

Вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке:

.

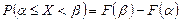Вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Функция f (х), равная производной функции распределения, характеризует плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины Х. Иногда ее называют дифференциальной функцией распределения.

f (x)=F¢(x).

Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.

Функция распределения выражается через функцию плотности следующим образом:

.

Геометрически f (х) есть площадь кривой распределения, лежащая левее точки х.

Свойства плотности распределения.

1) f (x)³0. Геометрически это означает, что вся кривая распределения лежит не ниже оси абсцисс.

2) 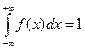. Геометрически это означает, что полная площадь, ограниченная кривой распределения и осью абсциссравна единице.

Назначение числовых характеристик – выразить в сжатой форме наиболее существенные особенности распределения. С помощью числовых характеристик существенно облегчается решение многих вероятностных задач. Часто удается решить задачу до конца, оставляя в стороне законы распределения и оперируя одними числовыми характеристиками.

Среди числовых характеристик случайных величин отметим те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.

Важнейшую роль играет математическое ожидание случайной величины, которое иногда называют средним значением случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

.

Для непрерывной случайной величины Х математическое ожидание выражается уже не суммой, а интегралом:

,

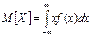где f (х) – плотность распределения величины Х.

Свойства математического ожидания.

1) М(С)=С, где С – некоторая постоянная величина.

2) М(СХ)=СМ(Х).

3) М(ХУ)=М(Х)∙М(У), где Х и У независимые случайные величины.

4) М(Х+У)=М(Х)+М(У), для любых случайных величин Х и У.

Модой случайной величины называется ее наиболее вероятное значение – для дискретной величины, и для непрерывной случайной величины – это значение, в котором плотность вероятности максимальна.

Медианой случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме:

Р(Х< Ме)=P(X> Me).

Геометрически медиана– это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Кроме характеристик положения употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик чаще всего применяются моменты.

Начальным моментом s-го порядка называется:

а) сумма вида 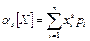для дискретной случайной величины;

б) интеграл вида 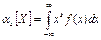для непрерывной случайной величины.

Нетрудно видеть, что математическое ожидание есть первый начальный момент.

Можно также сказать, что начальным моментом s-го порядка случайной величины Х называется математическое ожидание s-й степени этой случайной величины:

a_s[Х]=М[Х^s].

Центрированной случайной величиной 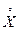, соответствующей величине Х, называется отклонение случайной величины Х от ее математического ожидания т_х: .

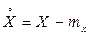Центральным моментом s-го порядка случайной величины Х называется математическое ожидание s-й степени соответствующей центрированной случайной величины:

m_s[Х]=М 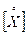=М[(Х– т_х)^s].

Центральный момент s-го порядка выражается:

а) суммой вида для дискретной случайной величины;

б) интегралом вида для непрерывной случайной величины.

Дисперсией случайной величины Х называется математическое ожидание квадрата соответствующей центрированной величины:

D[X]=M[ 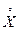²] =М[(Х– т_х)²].

Для непосредственного вычисления дисперсии служат формулы:

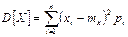и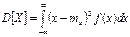

соответственно для дискретных и непрерывных величин. На практике часто используют формулу: D _x =a₂– m ² _x.

Свойства дисперсии.

1) D(С)=0, где С – некоторая постоянная величина.

2) D(СХ)=С²∙D(Х).

3) D(Х±У)= D(Х)+ D(У), где Х и У независимые случайные величины.

Дисперсия есть характеристика рассеивания, разбросанности значений случайной величины около ее математического ожидания. Для наглядной характеристики рассеивания удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такая величина называется средним квадратическим отклонением случайной величины Х:

.

Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних отклонений этих величин:

.

Основные распределения дискретных и непрерывных случайных величин будут даны на СРСП.

Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Дата добавления: 2014-11-26