
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 10. Статистические методы обработки экспериментальных данных
|
|
|
|
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.
Выборочной совокупностью или просто выборкой называется совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объем совокупности (выборочной или генеральной) есть число объектов этой совокупности.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Выборка должна быть репрезентативной (представительной), т.е. она должна правильно представлять пропорции генеральной совокупности.
На практике применяются различные способы отбора. Их можно разделить на два вида:
1.Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор.
Эмпирическая функция распределения является статическим аналогом теоретической функции распределения и имеет свойства функции распределения.
Если х 1, x 2,..., xn – последовательность наблюдаемых значений некоторой случайной величины Х (выборка из генеральной совокупности с функцией распределения F(x)). Каждому значению из выборки естественно поставить в соответствие «вероятность» равную 1/ n, тогда функция распределения F*(x) выборки определится как ступенчатая функция со скачками высотой 1/ n в каждой точке xi, 1£ i £ n. Если m – число выборочных значений, не превосходящих x, то, очевидно,
F*(x)=m / n
F*(x), таким образом, определяется как частота события Х< x в последовательности из n наблюдений. Из теоремы Бернулли следует, что F*(x) по вероятности сходится к F(x).
На практике выборки большого объема из непрерывных распределений обычно подвергаются группировке. По сгруппированным результатам наблюдений строят гистограмму (полигон частот), которая является статистическим аналогом плотности вероятностей случайной величины.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высота равна отношению P i / h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а на них строят прямоугольники площадью P i */ h.
В распоряжении исследователя, как правило, имеются данные выборки, полученные в результате n наблюдений. Задачей исследователя является нахождение приближенных значении для неизвестных параметров (оценивание параметров).
Пусть x =(x 1, x 2,..., xn) – данные наблюдения. Для оценки математического ожидания обычно служит среднее арифметическое значение вариант.
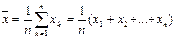
Для оценки дисперсии (выборочная дисперсия) применяется следующая формула:
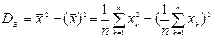
Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой s – средним квадратическим отклонением.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
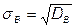 .
.
Оценка, определяемая одним числом, называется точечной оценкой. Оценка, определяемая двумя числами (концами интервала) называется интервальной.
Пусть 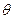 – неизвестный параметр распределения,
– неизвестный параметр распределения, 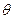 * – его точечная оценка. Было бы желательно, чтобы выполнялось неравенство:
* – его точечная оценка. Было бы желательно, чтобы выполнялось неравенство:
 ;
;
где 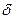 – некоторая маленькая величина,
– некоторая маленькая величина, 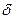 >0 (точность оценки). Так как
>0 (точность оценки). Так как 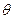 * – случайная величина (найденная на основе случайных ответных данных), то последнее неравенство всегда может быть нарушено, поэтому это неравенство может быть оценено только по вероятности, то есть при заданном значении
* – случайная величина (найденная на основе случайных ответных данных), то последнее неравенство всегда может быть нарушено, поэтому это неравенство может быть оценено только по вероятности, то есть при заданном значении 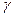 (надежность, доверительная вероятность) может быть найдено значение
(надежность, доверительная вероятность) может быть найдено значение 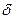 из неравенства
из неравенства
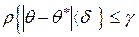 . (*)
. (*)
Обычно в качестве надежности выбирают одно из следующих стандартных значений: 0,95; 0,99; 0,9999 (это сокращает объем статистических таблиц). Полученный в результате решения неравенства (*) интервал называется доверительным интервалом.
Доверительный интервал для оценки математического ожидания нормального распределения (при известном балансе) находится по формуле:
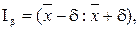
где баланс 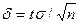 , а параметр t находится из условия 2Ф(t)=γ.
, а параметр t находится из условия 2Ф(t)=γ.
Основная литература: [1], [2], [3].
Дополнительная литература: [3], [4].
|
|
|
|
|
Дата добавления: 2014-11-26; Просмотров: 956; Нарушение авторских прав?; Мы поможем в написании вашей работы!