Тема 5. Формула полной вероятности, формула Байеса

Следствием теорем сложения и умножения является формула полной вероятности.

Теорема 1. Вероятность события А, которое может произойти совместно с одним из событий Н₁, Н₂, …, Н _п, образующих полную группу несовместных событий (эти события назовем гипотезами), равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А и вычисляется по формуле:

.

Доказательство. По условию появление события А означает осуществление одного, безразлично какого, из несовместных событий В ₁ А, В ₂ А, …, В­_пА. Используя теорему сложения, получим

Р (А)=Р(В ₁ А)+Р(В ₂ А)+…+Р(В­_пА). (*)

По теореме умножения вероятностей зависимых событий вычислим каждое из слагаемых

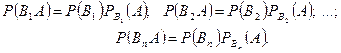
Подставив правые части этих равенств в (*), получим формулу полной вероятности

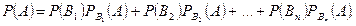
Следствием теоремы умножения и формулы полной вероятности является теорема гипотез или формула Байеса. Поставим следующую задачу.

Имеется полная группа несовместных гипотез Н₁, Н₂, …, Н _п. Вероятности этих гипотез до опыта известны и равны соответственно Р(Н₁), Р(Н₂), …, Р(Н _п). Произведен опыт, в результате которого наблюдено появление некоторого события А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события? Здесь по существу, речь идет о том, чтобы найти условную вероятность Р_А(Н _i) для каждой гипотезы. На этот вопрос отвечает формула Байеса:

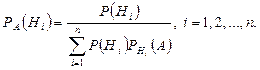
Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Тема 6. Схема Бернулли, локальная и интегральная теоремы Муавра–Лапласа, приближение Пуассона.

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

В разных независимых испытаниях событие А может иметь либо разные вероятности, либо одну и ту же. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.

Пусть производится п независимых испытаний, в каждом из которых событие А может появится либо не появится. Условимся считать, что вероятность события А в каждом испытании одна и та же, и равна р. Тогда вероятность ненаступления события А в каждом испытании постоянна и равна q =1– р.

Поставим перед собой задачу вычислить вероятность того, что при п испытаниях события А осуществится ровно т раз. Здесь не требуется, чтобы событие А повторилось ровно т раз в определенной последовательности. Например, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие события: .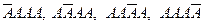

Искомую вероятность обозначим Р _п (т). Поставленную задачу можно решить с помощью формулы Бернулли, которая имеет вид:

.

Приведенная выше формула Бернулли при больших значениях п достаточно сложна, так как формула требует выполнения действий над громадными числами.

Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно т раз в п испытаниях, если число испытаний достаточно велико.

Для частного случая, а именно для р = 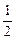, асимптотическая формула была найдена в 1730г. Муавром; в 1783г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, о которой пойдет речь, называют теоремой Муавра–Лапласа.

Локальная теорема Маувра–Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля, то вероятность Р _п­­ (т) того, что событие А появится в п испытаниях ровно т раз, приближенно равна (тем точнее, чем больше п) значению функции

.

Имеются таблицы, в которых помещены значения функции 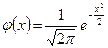, соответствующие положительным значениям аргумента пользуются теми же таблицами, так как функция j(х) четна.

Итак, вероятность того, что событие А появится в п независимых испытаниях ровно т раз, приближенно равна

.

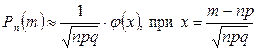Вновь предположим, что производится п испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0<p<1). Как вычислить вероятность Р_п(т₁, т₂) того, что событие А появится в п испытаниях не менее т₁ и не более т₂ раз? На этот вопрос отвечает интегральная теорема Лапласа.

Интегральная теорема Муавра–Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р _п (т ₁, т ₂) того, что событие А появится в п испытаниях от т ₁ до т ₂ раз, приближенно равна определенному интегралу

(*)

При решении задач, требующих применения интегральной теорема Муавра–Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 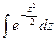не выражается через элементарные функции. В таблицах даются значения функции для положительных значений х и для х =0. Для отрицательных значений х можно воспользоваться той же таблицей, так как Ф(х) – функция нечетная. В таблицах также приводятся значения интеграла только лишь до х =5, для х >5 можно принять Ф(х)=0,5. Функцию Ф(х) часто называют функцией Лапласа.

Чтобы можно было пользоваться таблицей функции Лапласа, преобразовав выражение (*) так:

Асимптотическая формула Лапласа (локальная теорема) непригодна, если вероятность события мала (р£0,1). В этих случаях (п велико, р мало) прибегают к асимптотической формуле Пуассона.

Сделаем важное допущение: произведение пр сохраняет постоянное значение: пр =l. Тогда вероятность того, что при очень большом числе испытаний п, в каждом из которых вероятность события очень мала и равна р, событие наступит ровно т раз выражается формулой:

.

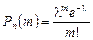Эта формула выражает закон распределения Пуассона вероятностей массовых и редких явлений.

Основная литература: [1], [2], [3].

Дополнительная литература: [3], [4].

Дата добавления: 2014-11-26