Плоскости и прямые в пространстве

Линии второго порядка

Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С (x ₀, y ₀) (случай В).

А В

Окружность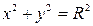
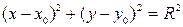
Эллипс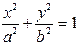
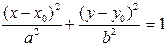
Гипербола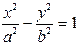
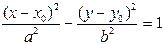
Парабола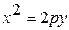

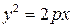
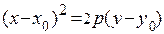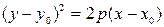
Пример 1. Пусть задано уравнение х² + y² - 4x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра?

Приведем данное уравнение к виду 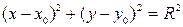. Выделим полный квадрат относительно х, прибавляя и вычитая число 4

x² + y² - 4x = (x² - 4x + 4) + y² - 4 = 0 или (x - 2)² + y² = 2². х₀ = 2, у₀ = 0, R = 2.

Пример 2. Дано уравнение кривой второго порядка 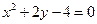. Определить тип кривой, найти ее параметры и сделать чертеж.

Решение. Сравнивая с табличными данными находим, что это парабола, вершига которой находится в точке С (x ₀, y ₀). приводим уравнение параболы к виду .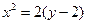

х₀ = 0, у₀ = 2, р = 1. Чертеж

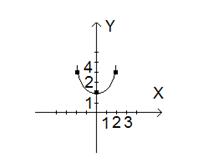
Рис. 2.

Пример. Даны координаты вершин пирамиды

А ₁(1,-2,-3), А ₂(-3,1,1), А ₃(4,3,-1), А ₄(3,2,2).

Составить: 1. Уравнение плоскости .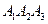

2. Уравнение перпендикуляра, опущенного из вершины А ₄ на грань .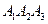

Решение. 1. Уравнение плоскости запишем, используя каноническое уравнение плоскости, проходящей через три данные точки:

.

Подставив координаты точек А ₁, А ₂, А ₃, получим

= .

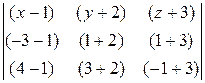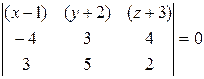Разложив последний определитель по элементам первой строки, будем иметь

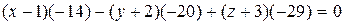
или

.

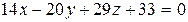2. Уравнение высоты пирамиды представим в виде канонической системы уравнений прямой, проходящей через заданную точку А ₄ с известным направляющим вектором 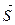. За направляющий вектор 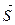возьмем нормальный вектор 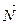плоскости 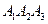, т.е. .

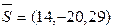Уравнение высоты: .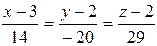

Примечание. Если бы в уравнении прямой один из знаменателей оказался нулевым, например

,

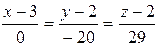то уравнение прямой следовало бы записать в виде пересекающейся системы плоскостей

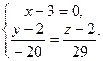
Наконец, если бы в уравнении прямой два знаменателя обратились в ноль, например,

,

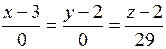это означало бы, что прямая является пересечением плоскосте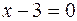й и 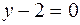и ее уравнением будет система

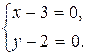
Контрольная работа 1. Задания.

1. Решить систему методами Крамера и последовательных исключений

1.1.	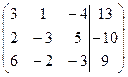.	1.11.	.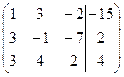
1.2	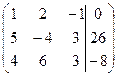.	1.12.	.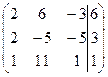
1.3.	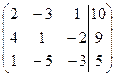.	1.13.	.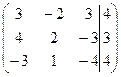
1.4.	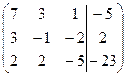.	1.14.	.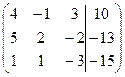
1.5.	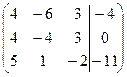.	1.15.	.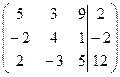
1.6.	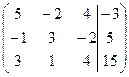.	1.16.	.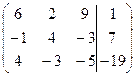
1.7.	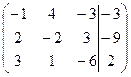.	1.17.	.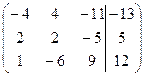
1.8.	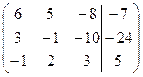.	1.18.	.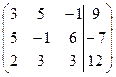
19.	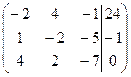.	1.19.	.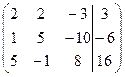
1.10.	.	1.20.	.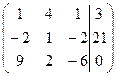

2. Даны координаты вершин пирамиды 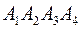. Средствами векторной алгебры найти:

1) длину ребра ;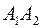

2) угол между ребрам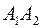и и ;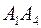

3) уравнение плоскости ;

4) уравнение перпендикуляра, опущенного из вершины 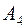на грань ;

5) площадь грани ;

6) объем пирамиды.

2.1.	,	,	,	.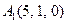
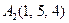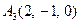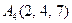2.2.	,	,	,	.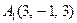
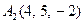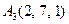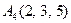2.3.	,	,	,	.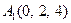
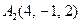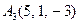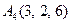2.4.	,	,	,	.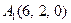
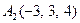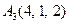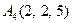2.5.	,	,	,	.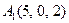
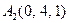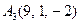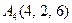2.6.	,	,	,	.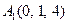
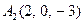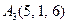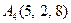2.7.	,	,	,	.
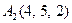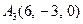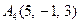2.8.	,	,	,	.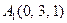
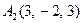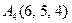2.9.	,	,	,	.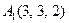
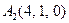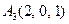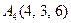2.10.	,	,	,	.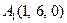
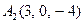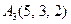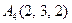2.11.	,	,	,	.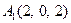
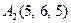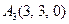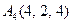2.12.	,	,	,	.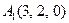
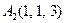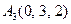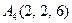2.13.	,	,	,	.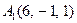
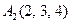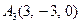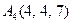2.14.	,	,	,	.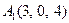
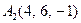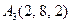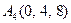2.15.	,	,	,	.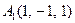
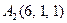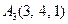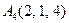2.16.	,	,	,	.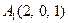
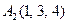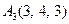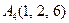2.17.	,	,	,	.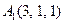
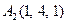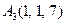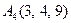2.18.	,	,	,	.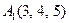
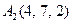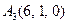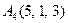2.19.	,	,	,	.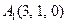
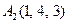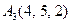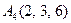2.20.	,	,	,	.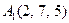

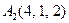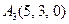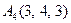В задачах 3.1 – 3.20 по аналитической геометрии сде­лать чертеж.

3. Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС, угол между ними, уравнения медианы СК и высоты АМ. Сделать чертеж

№	А	В	С	№	А	В	С
3.1.	(-5, 3)	(1,6)	(5, 1)	3.11	(1, 5)	(4, 0)	(-5,-4)
3.2.	(-7, 1)	(5, 0)	(2, 5)	3.12	(4, 2)	(2, 0)	(-1, 2)
3.3.	(5, 1)	(0, 4)	(-2, 2)	3.13	(0, -2)	(-2, 1)	(3, 4)
3.4.	(5, 2)	(-1, 0)	(3, 4)	3.14	(-1, 2)	(1, 1)	(-5, 3)
3.5.	(2, -2)	(3, -4)	(2, -1)	3.15	(4, 2)	(-3, 3)	(2, -1)
3.6.	(1, 0)	(2, 5)	(-1, 1)	3.16	(4, 4)	(5, 1)	(-1, 0)
3.7.	(0, -3)		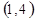(-2, -1)	3.17	(-2, 4)	(5, 1)	(0, -3)
3.8.	(-2, 1)	(3, 1)	(0, -2)	3.18		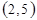(-1, 1)	(0,3)
3.9.	(-3, 3)	(7, 5)	(4, 1)	3.19	(1, 5)	(-5, 3)	(1,3)
3.10	(2, 0)	(5, -2)	(8, 2)	3.20		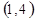(-2,1)	(0, -3)

3. Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС, угол между ними, уравнения медианы СК и высоты АМ. Сделать чертеж

№	А	В	С	№	А	В	С
3.1.	(-5, 3)	(10,6)	(1, 5)	3.11	(14, 5)	(4, 5)	(-5,-8)
3.2.	(-7, 1)	(5, 0)	(2, 5)	3.12	(10, 2)	(2, 0)	(5, -2)
3.3.	(5, 1)	(0, 3)	(-2, 4)	3.13	(0, -2)	(-2, 1)	(3, 1)
3.4.	(5, 2)	(-1, 0)	(4, 4)	3.14	(-1, 2)	(1, -1)	(-5, 1)
3.5.	(2, -2)	(3, -4)	(2, -1)	3.15	(4, 8)	(-3, 3)	(7, 5)
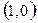
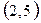
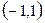
3.6.				3.16	(4, 4)	(5, 2)	(-1, 0)
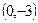
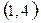
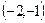
3.7.				3.17	(-2, 4)	(5, 1)	(0, 3)
3.8.	(-2, 1)	(3, 1)	(0, -2)	3.18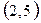
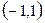
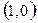
3.9.	(-3, 3)	(7, 5)	(4, 8)	3.19	(1, 5)	(-5, 3)	(10,6)
3.10	(2, 0)	(5, -2)	(10, 2)	3.20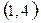

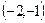
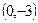
3. Указать тип кривой второго порядка, найти ее параметры и сделать чертеж.

4.1. 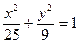.	4.11.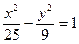
4.2.	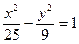4.12.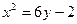
4.3.	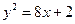4.13.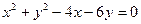
4.4.	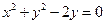4.14.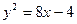
4.5.	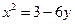4.15.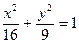
4.6.	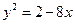4.16.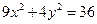
4.7.	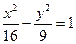4.17.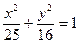
4.8.	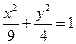4.18.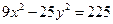
4.9.	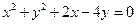4.19.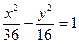
4.10.	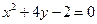4.20.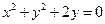

Дата добавления: 2014-11-09