
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производная. Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:
|
|
|
|
Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:
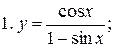
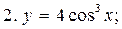
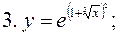 4.
4. 
Решение.
1. 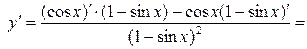
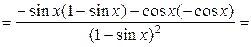
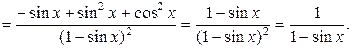
2. 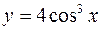 есть сложная функция.
есть сложная функция.
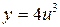 , где
, где 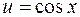 .
.
Производная сложной функции имеет вид
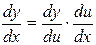 или
или 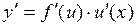 .
.
Следовательно,
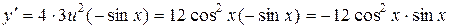 .
.
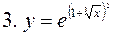 - сложная функция.
- сложная функция.
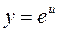 , где
, где 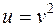 , а
, а 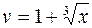 ,
,
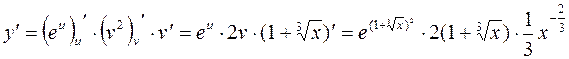 . 4.
. 4.
4. 
Функция 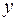 от независимой переменной
от независимой переменной 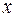 задана через посредство вспомогательной переменной (параметра t). Производная от
задана через посредство вспомогательной переменной (параметра t). Производная от 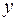 по
по 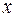 определяется формулой
определяется формулой
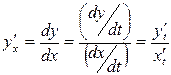 .
.
Находим производные от 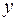 и
и 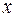 по параметру t:
по параметру t:
 ,
, 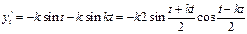 ,
,
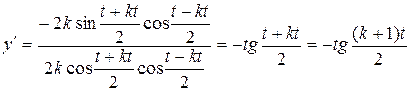 .
.
Пример 2. Составить уравнение касательной и нормали к кривой 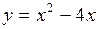 в точке, где
в точке, где 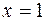 .
.
Решение. Уравнение касательной к кривой в точке 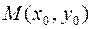
 ,
,
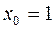 ,
, 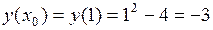 .
.
Для определения углового коэффициента касательной 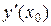 находим производную
находим производную
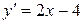 ,
,
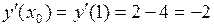 .
.
Подставляя значения 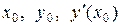 в уравнение, получим
в уравнение, получим
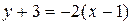 или
или 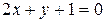 .
.
Уравнение нормали
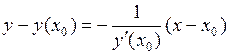 ,
,
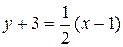 или
или 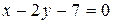 .
.
Пример 3. Точка совершает прямолинейное колебательное движение по закону 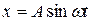 . Определить скорость и ускорение движения в момент времени
. Определить скорость и ускорение движения в момент времени 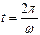 .
.
Решение. Найдем скорость 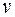 и ускорение а движения в любой момент времени t
и ускорение а движения в любой момент времени t
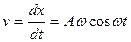 ;
; 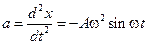 .
.
При 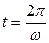
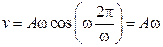 ,
, 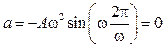 .
.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 620; Нарушение авторских прав?; Мы поможем в написании вашей работы!