
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследование поведения функций
|
|
|
|
Свойства дифференцируемых функций
Дифференциал, производные высших порядков
Пример 1. Найти дифференциалы функций
1. 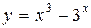 ; 2.
; 2. 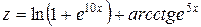 ,
,
вычислить  .
.
Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:
1.  ;
;
2. 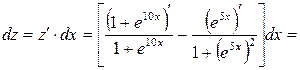
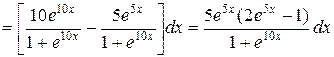 .
.
Пример 1. Найти пределы, используя правило Лопиталя.
1.  ; 2.
; 2. 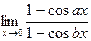 ; 3.
; 3. 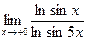 ; 4.
; 4.  .
.
Решение. Убедившись, что имеет место неопределенность  или
или  , применяем затем правило Лопиталя.
, применяем затем правило Лопиталя.
1. 

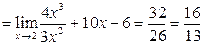 ;
;
2. 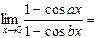
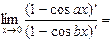


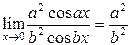 ;
;
здесь правило Лопиталя применено дважды.
3. 

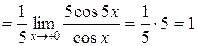 ;
;
4.  .
.
Пример 1. Исследовать и построить график функции
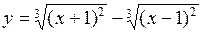 .
.
Решение.
1. Заданная функция определена и непрерывна на всей числовой оси
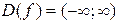 .
.
2. Функция нечетная, ибо  , ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для
, ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для  .
.
3. График функции пересекается с осями координат только в начале координат, так как 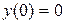 .
.
4. Исследуем функцию на наличие асимптот:
а) вертикальных асимптот график функции не имеет;
б) невертикальная асимптота имеет уравнение 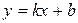 .
.
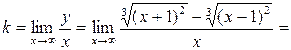

 ,
,

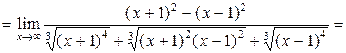
 .
.
Таким образом, уравнение асимптоты  .
.
5. Исследуем функцию на экстремум
 .
.
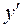 нигде не обращается в нуль;
нигде не обращается в нуль; 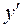 не существует в точках
не существует в точках 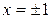 , которые являются критическими.
, которые являются критическими.
Исследуем знак производной на интервале [0; ∞) (рис.4)
 |

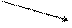 0 1
0 1
Рис. 4.
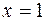 есть точка максимума,
есть точка максимума,  .
.
6. Исследуем график функции на выпуклость и вогнутость
 .
.
 в точке
в точке  ;
;  не существует в точках
не существует в точках 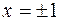 . Эти точки могут быть абциссами точек перегиба.
. Эти точки могут быть абциссами точек перегиба.
Исследуем знак второй производной на интервале [0; ∞) (рис.5)









 0 1
0 1
Рис. 5
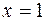 не является точкой перегиба.
не является точкой перегиба.
Основываясь на полученных результатах исследования, строим график функции на интервале [0; ∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0) (рис.6)

Рис. 6
Пример 2. Найти наибольшее и наименьшее значения функции
 на отрезке [-4; 4].
на отрезке [-4; 4].
Решение. 1. Найдем критические точки функции 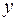 , лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:
, лежащие внутри отрезка [-4; 4], и вычислим ее значения в этих точках:  ;
;  в точках
в точках  и
и  . Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках:
. Эти точки лежат внутри отрезка [-4; 4] и являются критическими. Других критических точек нет, так как производная существует всюду. Значение функции в критических точках: 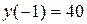 и
и 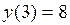 .
.
2. Вычислим значения функции на концах отрезка [-4; 4]: 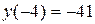 и
и 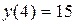 .
.
3. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции 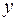 на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке
на отрезке [-4; 4] равно 40 и достигается ею во внутренней критической точке 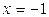 , а ее наименьшее значение равно -41 и достигается на левой границе отрезка
, а ее наименьшее значение равно -41 и достигается на левой границе отрезка 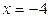 .
.
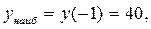
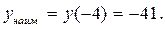
Функции нескольких переменных
Литература. [1], гл.VШ, § 1 - 4.
1. Частные производные.
Литература. [1], гл. VIII, § 5, 6, упр. 1-10.
Пример. 
1. Найти область определения функции.
2. Проверить, что 
3. Проверить, что 
Решение.
1. Под знаком логарифма может стоять только положительное выражение, следовательно
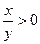
 или
или  .
.
Сделаем чертеж

Рис. 3.
2. При вычислении частной производной по  рассматриваем функцию
рассматриваем функцию  как функцию только от переменной
как функцию только от переменной  а при дифференцировании по
а при дифференцировании по 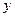 - как функцию только от
- как функцию только от 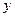 :
:
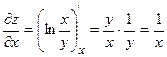 ,
,
 ,
,

3. При вычислении второй производной по  также рассматриваем функцию
также рассматриваем функцию  как функцию только от переменной
как функцию только от переменной  а при дифференцировании по
а при дифференцировании по 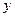 - как функцию только от
- как функцию только от 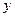 :
:
 ,
,
 ,
,
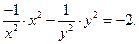
Контрольная работа 2. Задания
1. Найти точки разрыва функции, если они существуют. Сделать чертеж функции.
1.1. 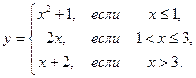
| 1.11. 
|
1.2. 
| 1.12. 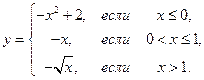
|
1.3. 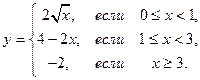
| 1.13. 
|
1.4. 
| 1.14. 
|
1.5. 
| 1.15. 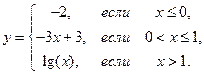
|
1.6. 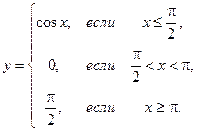
| 1.16. 
|
1.7. 
| 1.17. 
|
1.8. 
| 1.18. 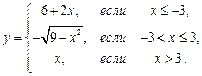
|
1.9. 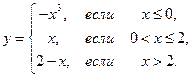
| 1.19. 
|
1.10. 
| 1.20. 
|
2. Найти производные  данных функций.
данных функций.
2.1. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 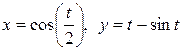 .
.
2.2. а) 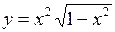 ; б)
; б) 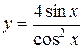 ;
;
в)  ; г)
; г) 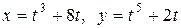 .
.
2.3. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2.4. а) 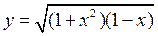 ; б)
; б)  ;
;
в) 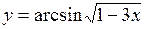 ; г)
; г)  .
.
2.5. а) 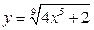 ; б)
; б) 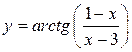 ;
;
в) 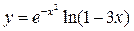 ; г)
; г)  .
.
2.6. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 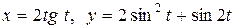 .
.
2.7. а) 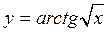 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2.8. а)  б)
б)  ;
;
в) 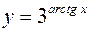 ; г)
; г) 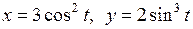 .
.
2.9. а) 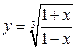 ; б)
; б) 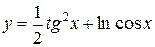 ;
;
в) 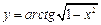 ; г)
; г)  .
.
2.10.а) 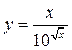 ; б)
; б) 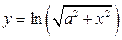 ;
;
в)  ; г)
; г) 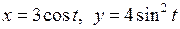 .
.
2.11.а) 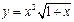 ; б)
; б) 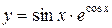 ;
;
в) 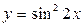 ; г)
; г) 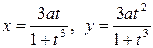 .
.
2.12.а)  ; б)
; б) 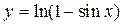 ;
;
в)  ; г)
; г)  .
.
2.13.а) 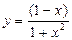 ; б)
; б) 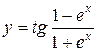 ;
;
в) 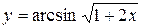 ; г)
; г)  .
.
2.14.а)  ; б)
; б) 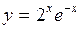 ;
;
в)  ; г)
; г) 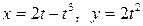 .
.
2.15.а)  ; б)
; б) 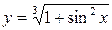 ;
;
в)  ; г)
; г) 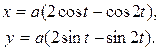
2.16.а)  ; б)
; б) 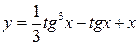 ;
;
в)  ; г)
; г) 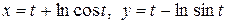 .
.
2.17.а)  ; б)
; б)  ;
;
в) 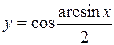 ; г)
; г) 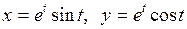 .
.
2.18.а) 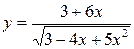 ; б)
; б) 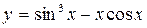 ;
;
в)  ; г)
; г)  .
.
2.19.а) 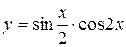 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2.20.а)  ; б)
; б) 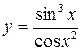 ;
;
в) 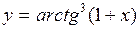 ; г)
; г) 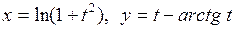 .
.
3.Найти указанные пределы, использую правило Лопиталя.
| а | б | |
| 3.1 | 
| 
|
| 3.2 | 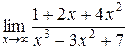
| 
|
| 3.3 | 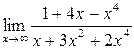
| 
|
| 3.4 | 
| 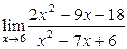
|
| 3.5 | 
| 
|
| 3.6 | 
| 
|
| 3.7 | 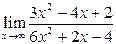
| 
|
| 3.8 | 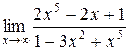
| 
|
| 3.9 | 
| 
|
| 3.10 | 
| 
|
| 3.11 | 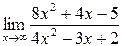
| 
|
| 3.12. | 
| 
|
| 3.13 | 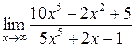
| 
|
| 3.14 | 
| 
|
| 3.15 | 
| 
|
| 3.16 | 
| 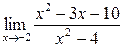
|
| 3.17 | 
| 
|
| 3.18 | 
| 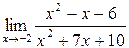
|
| 3.19 | 
| 
|
| 1.20. | 
| 
|
4. Найти интервалы монотонности и экстремумы функции.
4.1.  ; ;
| 4.11.  ; ;
|
4.2.  ; ;
| 4.12. 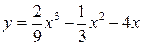 ; ;
|
4.3. 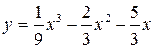 ; ;
| 4.13.  ; ;
|
4.4.  ; ;
| 4.14. 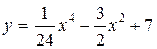 ; ;
|
4.5.  ; ;
| 4.15.  ; ;
|
4.6. 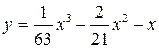 ; ;
| 4.16.  ; ;
|
4.7.  ; ;
| 4.17. 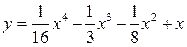 ; ;
|
4.8.  ; ;
| 4.18. 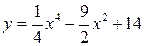 ; ;
|
4.9.  ; ;
| 4.19. 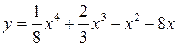 ; ;
|
4.10.  ; ;
| 4.20.  ; ;
|
5. Дана функция двух переменных
Проверить, удовлетворяет ли функция двух переменных 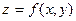 указанному дифференциальному уравнению первого порядка.
указанному дифференциальному уравнению первого порядка.
| 5.1 | 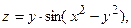 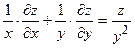
|
| 5.2 | 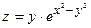 , , 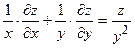
|
| 5.3 | 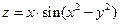 , , 
|
| 5.4 |  , , 
|
| 5.5 |  , , 
|
| 5.6 | 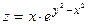 , , 
|
| 5.7 |  
|
| 5.8 | 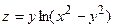 , , 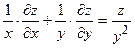
|
| 5.9 | 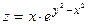 , , 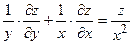
|
| 5.10. |  , , 
|
| 5.11 |  , , 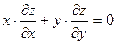
|
| 5.12 |  , , 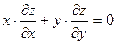
|
| 5.13 | 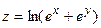 , , 
|
| 5.14 |  , , 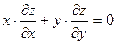
|
| 5.15 | 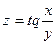 , , 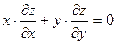
|
| 5.16 |  , , 
|
| 5.17 | 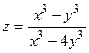 , , 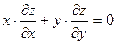
|
| 5.18 | 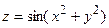 , , 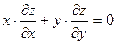
|
| 5.19 | 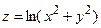 , , 
|
| 5.20 | 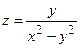 , , 
|
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 413; Нарушение авторских прав?; Мы поможем в написании вашей работы!