
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение системы трех линейных уравнений методами Крамера и Гаусса
|
|
|
|
Определители второго и третьего порядков.
Контрольная работа № 1
Для матрицы A размером 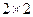 определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
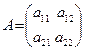 det(A) =
det(A) = 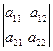 = a11 a22 – a12 a21.
= a11 a22 – a12 a21.
Для матрицы А размером  определитель находится по формуле
определитель находится по формуле
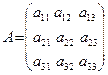 det(A) =
det(A) = 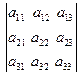 = a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
= a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
- a12 a21 a33 - a11a23 a32.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
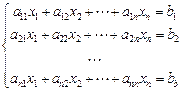
| 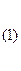
|
Вычислим определитель системы 
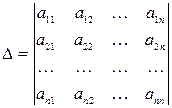
| 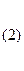
|
Как известно, если 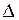 ¹0, то система (1) имеет решение, и при том единственное. Если
¹0, то система (1) имеет решение, и при том единственное. Если 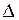 =0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
=0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
В дальнейшем мы будем предполагать, что 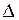 ¹0.
¹0.
1. Решение с помощью формул Крамера.
Если определитель системы 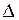 ¹0, то, согласно формулам Крамера, решение системы (1) можно представить в виде
¹0, то, согласно формулам Крамера, решение системы (1) можно представить в виде
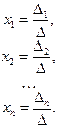
| 
|
Здесь
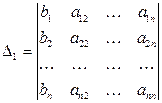 ; ;
| 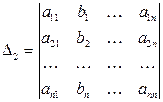 ; ;
| ||
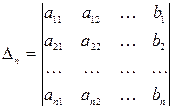 . .
| 
| ||
Определитель 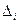 (i =1, 2,…, n) отличается от определителя системы
(i =1, 2,…, n) отличается от определителя системы 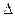 тем, что
тем, что 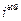 столбец
столбец 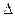 заменен столбцом из свободных членов, т.е. столбец
заменен столбцом из свободных членов, т.е. столбец 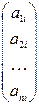 заменен на столбец
заменен на столбец 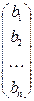 .
.
Пример. Дана расширенная матрица системы 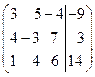 . Решить систему методом Крамера.
. Решить систему методом Крамера.
Решение. Запишем систему в стандартной форме
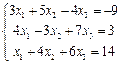 .
.
Определитель данной системы
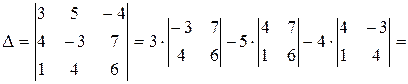
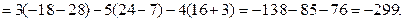
Вычислим определители 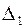 ,
, 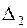 и
и 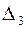 :
:
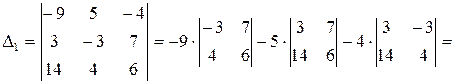
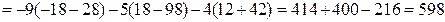 .
.

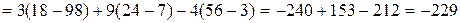 .
.
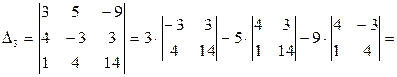
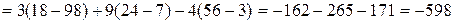 .
.
Решение системы: 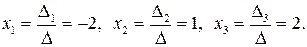
Для того чтобы убедиться в правильности решения, подставим эти значения 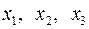 в исходную систему
в исходную систему
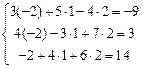 .
.
2. Решение методом Гаусса. Пусть есть система (1) с определителем  ¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
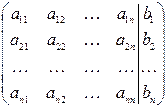 . .
| 
|
Метод Гаусса состоит в том, что система (1) с помощью ряда элементарных преобразований сводится к новой системе, расширенная матрица которой имеет вид
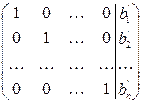 . .
| 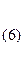
|
Т.е. в результате преобразований все коэффициенты матрицы 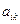 становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:
становятся равными нулю, кроме диагональных элементов, которые становятся равными единице: 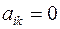 при
при 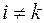 и
и 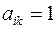 при
при 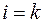 . Столбец свободных членов
. Столбец свободных членов 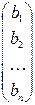 превращается в новый столбец
превращается в новый столбец 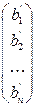 .
.
Если мы привели нашу матрицу к диагональному виду, то решение системы записывается очень просто:
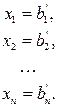
|
Таким образом, решение системы сводится к совершению элементарных преобразований, в результате которых расширенная матрица (5) превращается в расширенную матрицу (6).
К элементарным преобразованиям системы (1) относятся следующие:
1) перемена местами уравнений (т.е. перемена местами строк расширенной матрицы);
2) умножение или деление любого уравнения системы (1) на число, отличное от 0 (т.е. умножение или деление строки расширенной матрицы на число, отличное от 0);
3) изменение любого уравнения системы (1) путем прибавления к нему другого уравнения системы, умноженного на число, отличное от 0 (т.е. изменение строки расширенной матрицы путем прибавления к ней другой строки, умноженной на число, отличное от 0).
Пример. Найти решение системы методом Гаусса.
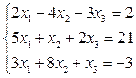 .
.
Решение. Определитель системы 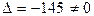 . Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
. Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
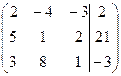 .
.
Далее мы будем приводить нашу матрицу к диагональному виду и выписывать ее вид после каждого шага преобразований.
1-й шаг. Разделим 1-ю строку матрицы на 2.
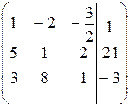 .
.
2-й шаг. 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:
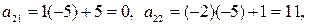

Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда

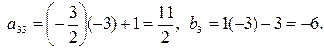
Расширенная матрица примет вид
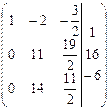 .
.
В результате первых 2-х шагов 1-й столбец 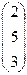 преобразовался в
преобразовался в 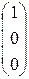 .
.
3-й шаг. Делим вторую строку на 11.
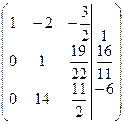 .
.
4-й шаг. 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда
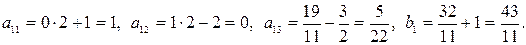
Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на (-14) и складываем ее с 3-й строкой, тогда
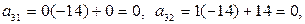
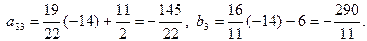
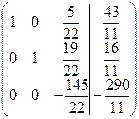 .
.
В результате 3-го и 4-го шагов 1-й столбец матрицы не изменился, а 2-й превратился в 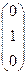 .
.
5-й шаг. Делим 3-ю строку на 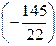
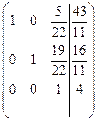 .
.
6-й шаг. 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 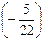 и складываем ее с 1-й строкой, тогда
и складываем ее с 1-й строкой, тогда
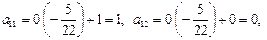
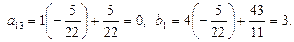
Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 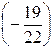 и складываем ее со 2-й строкой, тогда
и складываем ее со 2-й строкой, тогда
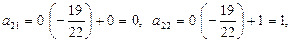
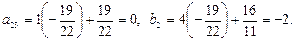
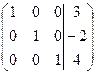 .
.
В результате 5-го и 6-го шагов 3-й столбец принял вид 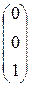 .
.
Таким образом, решение системы следующее:  Проверка
Проверка
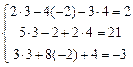
Таким образом, смысл метода Гаусса состоит в том, что сначала 1-й столбец исходной матрицы приводим к виду 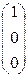 , затем 2-й - к виду
, затем 2-й - к виду 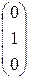 и, наконец, 3-й – к виду
и, наконец, 3-й – к виду  . При этом происходит преобразование столбца свободных членов.
. При этом происходит преобразование столбца свободных членов.
Решение методом исключений. Метод исключений является модификацией метода Гаусса и удобен для небольших систем.
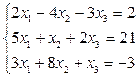 .
.
Умножим первое уравнение на коэффициент при х 1 из второго уравнения, т.е. на 5, а второе на коэффициент при х 1 из второго уравнения, т.е. на 2 и вычтем друг из друга. Потом умножим первое на коэффициент при х 1 из второго уравнения, т.е. на 3, а третье на 5 и снова вычтем
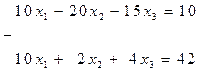
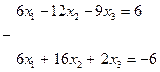
_______________________________ ___________________
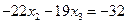
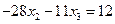
Поменяем в первом уравнении знаки и запишем подсистему
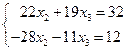
Умножим первое уравнение на 28, второе на 22 и сложим. Слагаемые с х 2 сократятся и мы получим уравнение для х 3
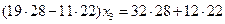
х 3 = 4, подставляя х 3 в первое уравнение подсистемы получим х 2
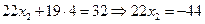 , х 2 = -2,
, х 2 = -2,
Подставляя х 2 и х 3 в первое уравнение системы найдем х 1
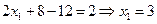
Объем вычислений при этом методе существенно меньше.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 1078; Нарушение авторских прав?; Мы поможем в написании вашей работы!