МАТЕМАТИКА. Приложения определенного интеграла

Приложения определенного интеграла

Несобственные интегралы

Определенный интеграл

Пусть на отрезке [a, b] задана непрерывная функция f(x).

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]

Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

x₀ < x₁ < x₂ < … < x_n

Тогда x₁ – x₀ = Dx₁, x₂ – x₁ = Dx₂, …,x_n – x_n-1 = Dx_n;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

[x₀, x₁] ® m₁, M₁; [x₁, x₂] ® m₂, M₂; … [x_n-1, x_n] ® m_n, M_n.

Составим суммы:

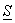_n = m₁Dx₁ + m₂Dx₂ + … +m_nDx_n =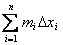

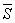_n = M₁Dx₁ + M₂Dx₂ + … + M_nDx_n =

Сумма 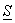называется нижней интегральной суммой, а сумма 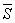– верхней интегральной суммой.

Т.к. m_i £ M_i, то 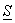_n £ 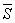_n, а m(b – a) £ 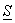_n £ 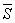_n £ M(b – a)

Внутри каждого отрезка выберем некоторую точку e.

x₀ < e₁ < x₁, x₁ < e < x₂, …, x_n-1 < e < x_n.

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].

S_n = f(e₁)Dx₁ + f(e₂)Dx₂ + … + f(e_n)Dx_n =

Тогда можно записать: m_iDx_i £ f(e_i)Dx_i £ M_iDx_i

Следовательно,

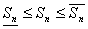
Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.Обозначим maxDx_i – наибольший отрезок разбиения, а minDx_i – наименьший. Если maxDx_i® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.

// Если 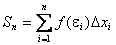, то

Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDx_i® 0 и произвольном выборе точек e_i интегральная сумма 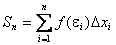стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]. Обозначение:

а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Определение: Если для функции f(x) существует предел 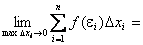то функция называется интегрируемой на отрезке [a, b].Также верны утверждения: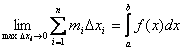

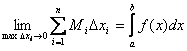
Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Свойства определенного интеграла.

1)

2)

3)

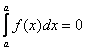
4) Если f(x) £ j(x) на отрезке [a, b] a < b, то

5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что

7) Для произвольных чисел a, b, c справедливо равенство:

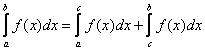
Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.

8)

Вычисление определенного интеграла.

Пусть в интеграле 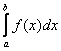нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.

Обозначим = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.

Аналогичную теорему можно доказать для случая переменного нижнего предела.

Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.

Теорема: (Теорема Ньютона – Лейбница)

Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то

это выражение известно под названием формулы Ньютона – Лейбница.Иногда применяют обозначение F(b) – F(a) = F(x) .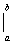

Замена переменных.

// Пусть задан интеграл 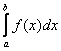, где f(x) – непрерывная функция на отрезке [a, b].

Введем новую переменную в соответствии с формулой x = j(t).

Тогда если

1) j(a) = а, j(b) = b

2) j(t) и j¢(t) непрерывны на отрезке [a, b]

3) f(j(t)) определена на отрезке [a, b], то

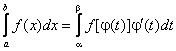
Тогда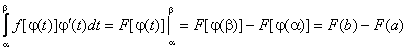

Пример.

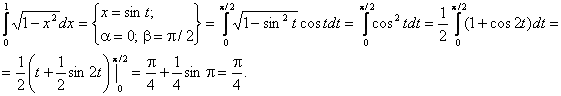
Интегрирование по частям.

Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

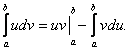
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:

.

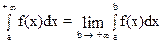Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+¥), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+¥). В противном случае про интеграл говорят, что он не существует, или расходится.

Аналогично определяются несобственные интегралы на интервалах
(-¥, b] и (-¥, +¥):

.

Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка [a,b], кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:

,

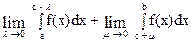если эти пределы существуют и конечны. Обозначение:

= .

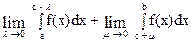Пример Вычислить интеграл .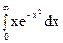

Решение. Подынтегральная функция определена и непрерывна при всех значениях х и, следовательно, имеет первообразную F(x)= .

По определению имеем: = .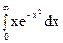

По формуле Ньютона-Лейбница,

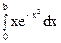= F(b) - F(0) = + = ;

= = .

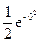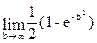Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур.

Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.Для нахождения суммарной площади используется формула .

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x², x = 2.

//

Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:

(ед²)

Нахождение площади криволинейного сектора.

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид r = f(j), где r - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а j - угол наклона этого радиус – вектора к полярной оси.

Площадь криволинейного сектора может быть найдена по формуле

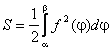
Вычисление длины дуги кривой.

//

y = f(x)

Длина ломаной линии, которая соответствует дуге, может быть найдена как .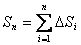

Тогда длина дуги равна .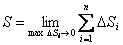

Из геометрических соображений:

В то же время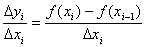

Тогда можно показать, что

Т.е.

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции получаем

,

где х = j(t) и у = y(t).

Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

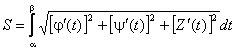
Если кривая задана в полярных координатах, то

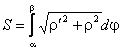, r = f(j).

Пример: Найти длину окружности, заданной уравнением x² + y² = r².

1 способ. Выразим из уравнения переменную у.

Найдем производную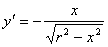

Тогда

Тогда S = 2pr. Получили общеизвестную формулу длины окружности.

2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r²cos²j + r²sin²j = r², т.е. функция r = f(j) = r, 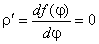тогда

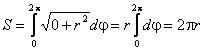
Вычисление объемов тел.

Вычисление объема тела по известным площадям его параллельных сечений.

Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х_i разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [x_i-1, x_i] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M_i и m_i.Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M_iDx_i и m_iDx_i здесь Dx_i = x_i - x_i-1.

Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно и .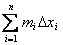

При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:

Таким образом, объем тела может быть найден по формуле:

// Пример: Найти объем шара радиуса R.

В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле .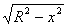

Тогда функция площадей сечений имеет вид: Q(x) = .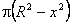

Получаем объем шара:

.

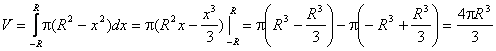Объем тел вращения.

Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.

y = f(x)

Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса 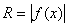, то объем тела вращения может быть легко найден по полученной выше формуле:

Площадь поверхности тела вращения.

Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных. Разобьем дугу АВ на n частей точками M₀, M₁, M₂, …, M_n. Координаты вершин полученной ломаной имеют координаты x_i и y_i. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DP_i. Эта площадь может быть найдена по формуле:

Здесь DS_i – длина каждой хорды.

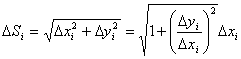Применяем теорему Лагранжа к отношению .

Получаем:

Тогда

Площадь поверхности, описанной ломаной равна:

Эта сумма не является интегральной, но можно показать, что

Тогда 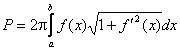- формула вычисления площади поверхности тела вращения.

Контрольные вопросы:

1.Определенный интеграл

2. Несобственные интегралы

3.Приложения определенного интеграла

Литература: [1, с. 370,415 ],[8, с.250-300]

Список рекомендуемой литературы:

1 Пискунов Н. С. Дифференциальные и интегральные исчисления. Часть I, II. 1972г.

2 Клетеник Д.В. Сборник задач по аналитической геометрии. М. 1992-1995г.

3 Курош А.Г. Высшая алгебра.

4 Демидович Б.П. Сборник задач и упражнении по мат. Анализ.

5 Берман Г.Н. Сборник задач по курсу математического анализа, М., Наука, 1975г.

6 Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, часть1, М., Высшая школа, 1998г.

7 Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, часть 2, М., Высшая школа, 1998г.

8 Шипачев В.С. Основы высшей математики, Высшая математика, 1989г.

9 Методические разработки кафедры

Методические указания и контрольные задания 1 и 2 для студентов заочной сокращенной формы обучения РИНПО

по специальностям:

262000.62 «Технология изделий легкой промышленности» по профилю «Технология швейных изделий»;

262200.62 «Конструирование изделий легкой промышленности», по профилю «Конструирование швейных изделий»;

100700.62 – Торговое дело;

100800.62 - Товароведение.

Мещерякова Г. П. Наумова Е. В. Мажара С. Ф.

Санкт-Петербург

УТВЕРЖДЕНО

на заседании методической комиссии

Регионального института непрерывного обучения

протокол № 1 от 14. 09. 2012

Рецензент

Н. В. Дробатун

Оригинал подготовлен составителями и издан в авторской редакции

Подписано в печать______ Формат 60х80 1/16.

Печать трафаретная. Усл. печ. л. 1,3 _. Тираж _ 100 _. Заказ ___

Электронный адрес: http://alt-rinpo.sutd.ru/ Отпечатано в типографии СПГУТД.

191028, Санкт - Петербург, ул. Моховая, 26

При выполнении контрольной работы на титульном листе указывается:

фамилия, имя, отчество;

номер студенческого билета;

название дисциплины, номер контрольной работы, номер варианта.

Номер варианта соответствует последней цифре номера студенческого билета.

Перечень контрольных заданий по методичке кафедры математики

КОНТРОЛЬНАЯ РАБОТА N 1 (методичка к/р 1,2)

Нечетный год поступления N 1(1 -10), 2(1 – 10), 3(1 – 10), 4(1 – 10).

Четный год поступления N 1(11 -20), 2(11 – 20), 3(11 – 20), 4(11 – 20), 5(11-20).

КОНТРОЛЬНАЯ РАБОТА N 2 (методичка к/р 1,2)

Нечетный год поступления N 1 (1 -10), 2 (1 - 10), 3 (1 - 10), 4 (1 - 10).

Четный год поступления N 1 (11 -20), 2 (11 - 20), 3 (11 - 20), 4 (11 - 20), 5(11 - 20).

Дата добавления: 2014-11-09