Преобразователи кодов

Сумматор одноразрядных десятичных чисел.

Так как один разряд десятичных чисел представляется четырьмя разрядами двоичных чисел, то сумматор одноразрядных десятичных чисел будет содержать 4 последовательно включенных сумматора одноразрядных двоичных чисел. Схема и условное графическое обозначение одноразрядного сумматора десятичных чисел показаны на рис. 9.11а и рис. 9.11б соответственно.

а) б)

Рис. 9.11. Схема и условное графическое обозначение одноразрядного

сумматора десятичных чисел

Для преставления информации в цифровой технике применяют различные цифровые коды. В ЭВМ при выполнении операций используются несколько разновидностей двоичных кодов: прямой, обратный, дополнительный и т.д. В цифровых системах связи применяют, например, коды с проверкой четности, коды Хемминга. Такие коды уменьшают вероятность появления ошибок и позволяют даже их исправлять.

Например,в процессоре преобразователь прямого кода в обратный отрицательное двоичное число X по значению знакового разряда (Z=1) переводит в обратный код 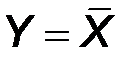.Положительное число (Z=0) он передает на выход без изменения 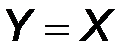. Эту логическую функцию в каждом разряде выполняет логическое устройство “Исключающее ИЛИ” . В цифровых системах всегда возникает необходимость в преобразовании информации из одного кода в другой. Эту логическую функцию выполняют преобразователи кодов. К преобразователям кодов относятся и шифраторы, и дешифраторы. На рис. 9.12 приведены УГО преобразователя кодов, шифратора и дешифратора соответственно.

DD1 DD2 DD3

Рис. 9.12. УГО преобразователя кодов, шифратора и дешифратора

9.8.8. Шифраторы и дешифраторы.

Шифратором (кодером) называется КЛУ, которое преобразует M -разрядный код в N -разрядный двоичный код, причем . Шифратор каждой из 2 ^M комбинации входных переменных однозначно ставит в соответствие набор из 2 ^N выходных переменных. Поскольку , то для передачи цифровой информации на выходе шифратора требуется меньше линий связи, т.е. шифратор производит “сжатие” информации.

Рассмотрим принцип работы шифраторов на примере шифратора из 10 в 4, который преобразует одноразрядные десятичные числа от 0 до 9 в прямой двоично-десятичный код. Это КЛУ имеет 10 входов и 4 выхода. При подаче 1 на один из 10 входов на выходе формируется 4-х разрядный прямой двоичный код, соответствующий номеру входа, на который был подан уровень 1.

Характер функционирования устройства задает таблица истинности (табл. 9.3). Используя таблицу истинности можно записать следующие алгебраический выражения:

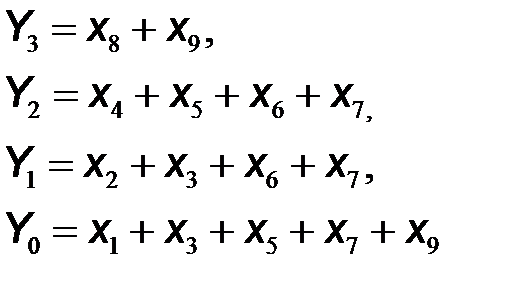
На рис. 9.13 приведена соответствующая логическая схема шифратора из 10 в 4.

Таблица 9.3

Таблица истинности шифратора из 10 в 4

№

x9

x8

x7

x6

x5

x4

x3

X2

x1

x0

Y3

Y2

Y1

Y0

Рис. 9.13. Логическая схема шифратора из 10 в 4

Дешифраторы (декодеры) – это КЛУ, которые информацию, представленную в виде двоичного кода преобразуют в исходный М-разрядный код. Дешифраторы выполняют операцию обратную шифраторам.

В цифровых системах дешифраторы часто исполняют роль “детектора”. Они распознают кодовые комбинации и выдают нужную информацию. Дешифраторы входят в состав исполнительных устройств и в зависимости от входного кода команды формируют сигнал управления для других блоков цифровых систем. Так, например в ЗУ по коду адреса дешифратор вырабатывает сигнал на подключение к шине данных ячейки памяти с указанным номером.

Для индикации одноразрядных десятичных чисел на световых табло, в цифровых измерительных приборах, в калькуляторах широко используются семисегментные индикаторы. Для их работы 4-х разрядный двоично-десятичный код с помощью дешифратора из 4 в 7 преобразуется в 7 выходных функций. Рассмотрим принцип работы такого дешифратора. Вид семисегментного индикатора показан на рис. 9.14. Его сегменты пронумеруем, как показано на рис. 9.14, а их состояние будем описывать логическими функциями (Y_n, n = 1, 2, 3, 4, 5, 6, 7).

Рис. 9.14. Общий вид семи сегментного индикатора

Пусть логическая функция равна нулю (Y =0) в случае, когда сектор светится, и Y =1 – когда сектор не светится. Логику работы дешифратора описывает таблица истинности, которая представлена в таблице 9.4.

Таблица 9.4

Таблица истинности дешифратора из 4 в 7

X3

X2

X1

X0

Y1

Y2

Y3

Y4

Y5

Y6

Y7

mi

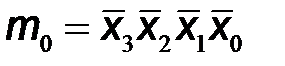
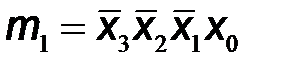
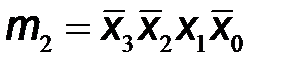
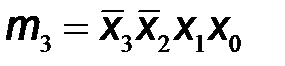
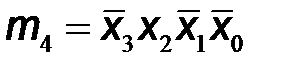
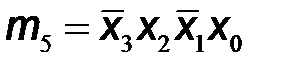
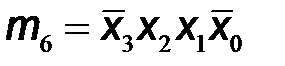
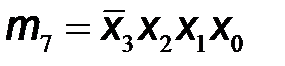
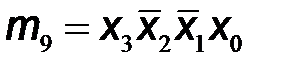
Используя обозначения логических произведений m_i на каждом из наборов входных переменных, которые приведены в последнем столбце таблицы, выходные логические функции запишем в следующем виде

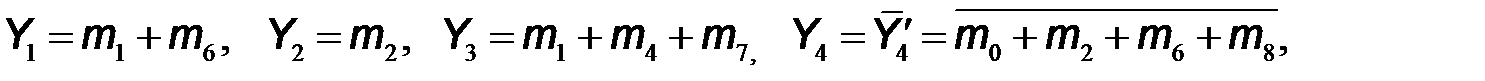
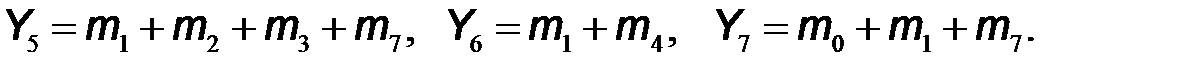
Из таблицы истинности следует, что логическая функция принимает значение логической единицы на шести наборах входных переменных и равна логическому нулю на четырех наборах. Поэтому для уменьшения количества слагаемых сначала записали выражение для ее инверсии: 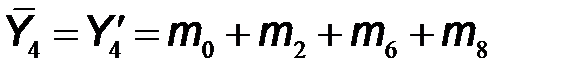, а затем, используя двойное отрицание, логическую функцию 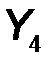представили как 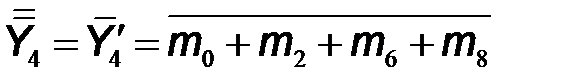. Вариант логической схемы дешифратора из 4 в 7, который соответствует приведенным формулам без упрощения алгебраического выражения (оптимизации) показан на рис. 9.15.

Рис. 9.15. Логическая схема дешифратора из 4 в 7

9.8.9. Мультиплексоры и демультиплексоры.

Мультиплексоры – это КЛУ, выполняющие управляемую передачу данных из нескольких источников (каналов) в один выходной канал. Мультиплексоры имеют две группы входов: информационные (D₀, D₁,…, D_N) и адресные (A₀, A₁, …, A_M). Количество информационных входов связаны с разрядностью адресных входов соотношением N=2^M.

Принцип работы мультиплексора состоит в следующем: К выходному каналу подключается информационный входной канал, номер которого совпадает с кодом адреса.

Для примера, синтезируем мультиплексор с двухразрядным адресом. Данному словесному описанию работы мультиплексора соответствует таблица истинности (рис. 9.16а). По таблице истинности записываем алгебраическое выражение в виде суммы логических произведений, состоящих из адресных кодов, умноженных на значение выходной функции:

.

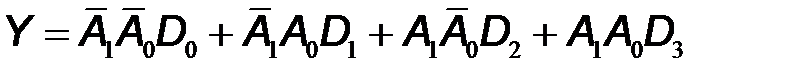Здесь под значением выходной функции подразумеваются входные данные, поступающие по входному каналу, номер которого совпадает с кодом адреса. Полученным алгебраическим выражениям соответствует логическая схема, показанная на рис. 9.16б. УГО мультиплексора представлено на рис. 9.16в.

   

№ набора	A1	A0	Y
			D0 D1 D2 D3

 

а)

б)

в)

Рис. 9.16. Таблица истинности, схема и УГО мультиплексора

с двухразрядным адресным входом

Демультиплексор – это КЛУ, которое выполняет управляемую передачу данных от одного источника информации в один из нескольких выходных каналов. Демультиплексор имеет один информационный вход, M -разрядный адресный вход и N выходных каналов. Количество информационных выходных каналов определяется разрядностью адресных входов соотношением N=2^M. Принцип работы демультиплексора состоит в следующем. По коду адреса информационный входной канал подключается к выходному каналу, номер которого совпадает с кодом адреса, т.е. демультиплексор имеет N выходных функций. Данному словесному описанию работы демультиплексора в случае двухразрядного адресного входа соответствует таблица истинности (рис. 9.17а). Как видно из таблицы истинности логика работы демультиплексора описывается алгебраическими выражениями в виде логических произведений, состоящих из адресных кодов, умноженных на значение входной функции:

.

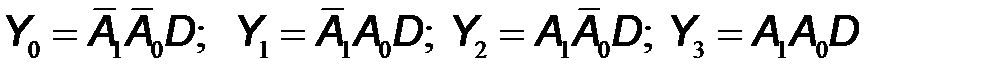Полученным алгебраическим выражениям соответствует логическая схема, показанная на рис. 9.17б. УГО демультиплексора представлено на рис. 9.17в.

   

№ набора	A1	A0	Y0	Y1	Y2	Y3
			D	-	-	-
			-	D	-	-
			-	-	D	-
			-	-	-	D

   

а)

б)

в)

Рис. 9.17. Таблица истинности, схема и УГО демультиплексора

с двухразрядным адресным входом

Дата добавления: 2014-11-16