Определение линейных и угловых кинематических величин

Частицы

Применение механических представлений к описанию движения одной

Основные идеи, понятия, модели, законы механики

Современная механика исходит из общефизических пространственно - временных представлений, т.е. считает пространство - время относительным, непрерывным, однородным, изотропным. Механическое движение подчиняется всем общефизическим законам, а также ряду специфических для механики законов.

Основной задачей механики является определение состояния частицы или системы частицы в любой момент времени по известному состоянию в какой-либо момент времени и закону изменения состояния во времени, называемому законом движения. Состояние частицы в механике определяется ее радиусом - вектором и импульсом, состояние системы частиц определяется радиусами - векторами и импульсам всех частиц системы. Такое определение состояния возможно, т.к. характерными объектами для механики являются макротела, момент импульса которых много больше постоянной Планка. Поэтому измерение координат существенно не изменяет импульса, не “возмущает” состояние макротела. Таким образом, можно говорить о координате и импульсе частицы и системы частиц в каждый момент времени, т.е. о кинематическом описании движения с помощью кинематических уравнений, о траектории, скорости, ускорении. Для динамического описания движения нужно учесть взаимодействия. Механика изучает гравитационные и электромагнитные взаимодействия в их макроскопических проявлениях. В процессе взаимодействия изменяются импульс, момент импульса, энергия частицы и системы частиц, причем скорость изменения импульса - есть равнодействующая сила, действующая на частицу или систему частиц, скорость изменения момента импульса равна моменту равнодействующей силы, скорость изменения энергии равна мощности. Эти соотношения наряду с законами сохранения импульса, момента импульса, энергии свободных частиц и изолированных систем частиц составляют основу механической схемы описания движения.

Рассмотрим механическое движение макротела, которое можно считать одной частицей в инерциальной системе отсчета с малой скоростью, т.е. .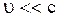

Пусть в инерциальной системе отсчета имеем частицу М (рис. 2.1). Положение ее в пространстве характеризуется радиусом - вектором 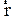, причем:

, (2.1)

где - единичные орты, - координаты частицы М. Радиус - ве-ктор проводится из начала системы отсчета к данной частице М, модуль его

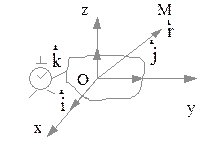
Рис. 2.1

равен: , (2.2)

где - независимые переменные. Число независимых переменных, характеризующих положение физической системы в пространстве, называют числом степеней свободы . Для данной частицы .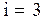

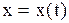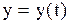Если частица движется, то ее координаты и радиус - вектор изменяются со временем: или ; ; . (2.3)

Это кинематические уравнения движения в общем виде. При движении частицы конец радиус - вектора описывает линию, которую называют траекторией. Пусть в момент времени 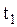частица занимала положение 1 и имела радиус - век-тор 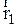, а в момент времени 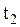- положение 2 с радиусом - вектором (рис.2.2).

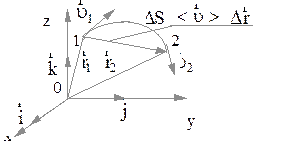
Рис. 2.2

Тогда расстояние, отсчитанное вдоль траектории, равно длине пути 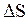, а вектор, проведенный из начальной в конечную точку движения называют вектором перемещения . Из рис. 2.2 видно, что:

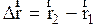. (2.4)

Длина пути и перемещение могут быть равны лишь для прямолинейного движения частицы в одну сторону, либо при очень малом времени движения. Можно показать, что 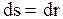. Угол поворота радиуса - вектора за время движения 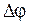называют угловым перемещением. Если , то можно считать угловое перемещение вектором, направленным перпендикулярно плоскости, в которой лежит и , по правилу правого винта. Согласно правилу винта, если сопоставить поворот от к повороту правого винта, то направление поступательного движения винта дает направление вектора углового перемещения (рис. 2.3).

Рис. 2.3

Так, если считать, что движение частицы происходит в плоскости 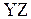(рис. 2.2), то 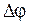будет направлен по оси 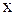в область отрицательных значений .

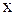При движении частицы по окружности численное значение ее радиуса - вектора равно радиусу окружности, а длина пройденного пути 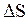связана с угловым перемещением известным из геометрии соотношением:

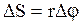. (2.5)

Можно показать справедливость равенства

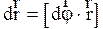, (2.6)

устанавливающего связь векторов линейного и углового перемещений частицы. Быстроту и направление движения характеризуют скоростью, причем различают линейные скорости (среднюю путевую, среднюю, мгновенную) и угловые скорости (среднюю, мгновенную). Средняя путевая скорость числено равна отношению длины пути 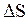к промежутку времени 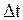, за который пройден путь 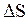: 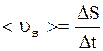. (2.7)

Средняя скорость 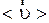числено равна отношению перемещения к промежутку времени, за который это перемещение произошло, направлена 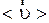как перемещение: . (2.8)

Мгновенная скорость 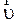числено равна первой производной от радиуса - вектора по времени и направлена по касательной в каждой точке траектории:

. (2.9)

Мгновенную скорость можно представить в виде:

, (2.10)

где

- (2.11)

проекции вектора 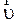на координатные оси.

Средняя угловая скорость числено равна угловому перемещению за единицу времени, направлена как угловое перемещение:

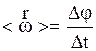. (2.12)

Мгновенная угловая скорость 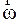числено равна первой производной от угла поворота по времени:

. (2.13)

Направлена мгновенная угловая скорость 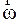как угловое перемещение. Разделив (2.6) на 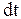и учитывая (2.9) и (2.13), получим формулу связи линейной и угловой скоростей: . (2.14)

На рисунке 2.4 векторы 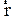и 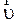лежат в плоскости , тогда согласно правилу правого винта вектор 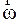направлен по оси .

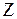В системе СИ единицы измерения линейной скорости - м/с, а угловой скорости - рад/с.

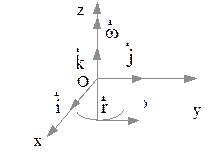
Рис 2.4

Изменение скорости со временем характеризуют ускорением. Различают линейные ускорения (среднее, мгновенное, тангенциальную и нормальную составляющие их) и угловые ускорения (среднее, мгновенное). Среднее ускорение 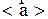числено равно отношению изменения скорости к промежутку времени, за который произошло это изменение:

, (2.15)

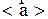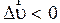направлено как , если и против , если . Мгновенное ускорение 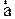равно первой производной от вектора скорости или второй производной от радиус - вектора по времени:

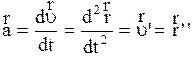. (2.16)

Мгновенное ускорение можно представить в виде

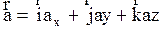, (2.17)

где 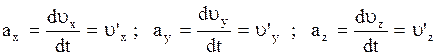- (2.18)

проекции вектора 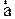на координатные оси. Ускорение характеризует изменение как модуля, так и направления скорости. Разложим 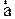на две составляющие, одна из которых оценивает изменение численного значения, другая - изменение направления скорости в единицу времени. Для этого представим скорость в виде: , (2.19)

где 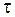- единичный вектор направления 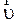и подставим (2.19) в (2.16):

. (2.20)

Можно показать, что 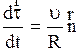, (2.21)

причем 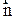- единичный вектор перпендикулярный - радиус кривизны траектории в каждой точке ее. Подставим (2.21) в (2.20):

, (2.22)

, (2.23)

где 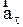- тангенциальная составляющая ускорения, характеризует изменение численного значения скорости в единицу времени, равно первой производной от модуля скорости по времени и направлено, как и мгновенная скорость, по касательной в каждой точке траектории.

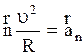, (2.24)

где - нормальная (центростремительная) составляющая ускорения, характеризует изменение направления скорости в единицу времени, числено равна квадрату модуля скорости, деленному на радиус кривизны траектории в данной точке; направленно перпендикулярно 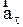к центру кривизны траектории. Векторная сумма 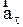и (рис. 2.5) позволяет определить численное значение и направление полного ускорения :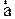

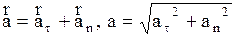^. (2.25)

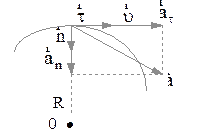
Рис 2.5

Среднее угловое ускорение числено равно отношению изменения угловой скорости к промежутку времени, за который это изменение произошло:

, (2.26)

направлено как угловая скорость, если , и против угловой скорости, если 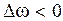. Мгновенное угловое ускорение числено равно первой производной от угловой скорости по времени или второй производной от углового перемещения по времени:

. (2.27)

Направление совпадает с направлением 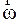при 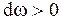и противоположно 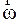, если 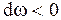. Для установления связ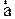и и продифференцируем (2.14) по времени:

. (2.28)

Подставляя уравнения (2.9), (2.16), (2.27) в (2.28) получим:

, (2.29)

где 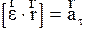, (2.30)

т.к. подставляя уравнения (2.14) в (2.23) получим (2.30)

, (2.31)

т.к. подставляя (2.14) в (2.24), получим (2.31).

В системе СИ единицы измерения линейного ускорения - 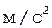, а углового ускорения - рад/c². Рассмотренные кинематические величины сведем в общую таблицу 2.1.

Таблица 2.1

Дата добавления: 2014-11-16