Законы механического движения системы частиц

Частиц

Определение физических величин, описывающих движение системы

Частиц

Применение механических представлений к описанию движения системы

Основные законы механического движения частиц

Систе-ма отсче-та	Скоро-сть частицы u, м/с	Моде-ль - частица	Законы	движен	ия
			Простран	ство	Время
			однородно	изотропно	однородно
ине-		свобо-дная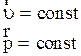
рци- аль-		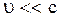несво-бодная
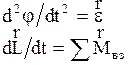
ные		свобо-дная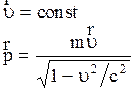
		несво-бодная
не- инер-		свобо-дная
ци- аль- ная		несво-бодная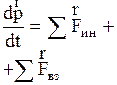

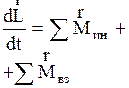
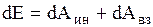
Система частиц - совокупность двух и более частиц, называемых внутренни ми. Система частиц называется изолированной (замкнутой), если она не взаимодействует с внешними частицами, не входящими в систему. Система частиц называется неизолированной, если она взаимодействует с внешними частицами, Внутренние частицы системы могут либо взаимодействовать, либо не взаимодействовать между собой. Примером системы частиц с жесткой связью между внутренними частицами является модель абсолютно твердого тела, у которого расстояния между частицами не изменяется во время движения.

В физике изучают три вида механического движения системы частиц точек: поступательное, вращательное, колебательное. Движение называют поступательным, если прямая, соединяющая две любые частицы системы, остается параллельной самой себе во все время движения. Вращательным называют движение системы, все частицы которой описывают окружности с центрами на одной прямой, называемой осью вращения. Движение системы называют колебательным, если значения физических величин, характеризующих движение, повторяются через некоторые промежутки времени.

Состояние системы частиц в механике определяется радиус-векторами и импульсами всех частиц системы в данный момент времени: . Характеристики системы определяются характеристиками частиц, входящих в данную систему. Важным понятием для системы частиц является понятие центра инерции системы-точки, радиус-вектор, скорость и ускорение которой определяется по формулам:

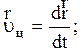
, (2.3.1)

где m - масса системы, равная сумме масс частиц системы: 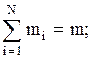поскольку масса обладает аддитивностью, как и ряд других физических величин. Масса системы частиц есть мера инерционных, гравитационных свойств и полной энергии системы.

Импульс системы частиц 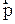равен геометрической сумме импульсов всех частиц системы: . (2.3.2)

Импульс также аддитивен. Выразим импульс системы через скорость центра инерции системы: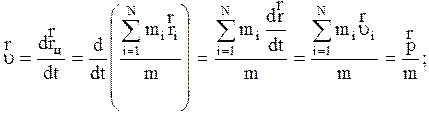

отсюда (2.3.3)

Момент инерции системы частиц относительно какой-либо оси вращения равен сумме моментов инерции всех частиц системы относительно той же оси:

(2.3.4)

Момент инерции, как видно, также аддитивная величина. Если вращать систему частиц относительно другой оси, то ее момент инерции будет другим, т.к. частицы системы будут находиться на других расстояниях от данной оси вращения. Следовательно, момент инерции системы характеризует распределение ее массы относительно оси вращения. В физике чаще всего рассматривают вращение однородных абсолютно твердых тел правильной геометрической формы относительно их осей симметрии. В таких случаях моменты инерции рассчитаны. Например:

а) момент инерции шара равен (рис. 2.3.1 а),

б) момент инерции сплошного цилиндра: (рис. 2.3.1 б),

в) момент инерции стержня: (рис. 2.3.1 в).

Рис. 2.3.1

Если известен момент инерции системы относительно оси, проходящей через цент масс системы 0₁0₂, то можно определить момент инерции этой системы относительно любой оси вращения 0₃0₄, параллельного первой по теореме Штейнера 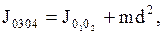где d - расстояние между осями, которое для рассматриваемого случая равно половине длины стержня, следовательно

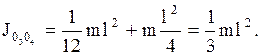
Момент импульса системы частиц равен геометрической сумме моментов импульса всех частиц системы:

. (2.3.5)

Для абсолютно твердого тела, вращающегося вокруг неподвижной оси, направление и численное значение угловых скоростей всех частиц тела одинаковы, поэтому момент импульса тела относительно этой оси с учетом (2.3.4) и (2.3.5) равен: 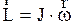, (2.3.6)

где J - момент инерции тела относительно той же оси вращения. Если абсолютно твердое тело кроме вращения вокруг определенной оси 0₁0₂ поступательно движется по замкнутой криволинейной траектории, то такое тело обладает как собственным моментом импульса относительно оси вращения 0₁0₂ равным , так и орбитальным моментом импульса относительно центра кривизны траектории, равным Например, наша планета Земля вращается вокруг собственной оси и движется по эллипсу вокруг Солнца, поэтому момент импульса Земли .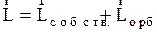

Если система частиц не изолирована, т.е. взаимодействует с другими системами или внешними частицами, то мерой взаимодействия в механике является сила 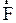, которая характеризуется численным значениям, направлением и точкой приложения. Векторное произведение радиус-вектора точки приложения силы и вектора силы называют моментом силы относительно точки 0 - начала системы отсчета:

. (2.3.7)

Направлен момент силы перпендикулярно плоскости, в которой лежат 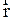и 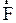, по правилу правого винта. На рис. 2.3.2 сила F приложена в точке Q системы частиц, причем 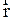и лежат в плоскости XY, тогда момент силы М относительно точки О направлен по оси Z. Проекции момента силы на оси координат называют моментами силы относительно осей X, Y, Z.

Рис. 2.3.2

Произведение силы на время ее действия называют импульсом силы 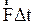, а произведение момента силы на время его действия называют импульсом момента силы .

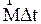Работа А есть величина, характеризующая процесс изменения состояния системы частиц в результате силового взаимодействия данной системы с другими системами. Если на систему частиц действует сила и при этом центр масс перемещается на , то совершаемая работа равна скалярному произведению и : . (2.3.8)

Работа силы на большом участке траектории движения системы частиц равна:

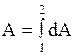, (2.3.9)

где 1 и 2 - начальное и конечное положения центра масс системы. Если система частиц повернулась относительно какой-либо оси на , под действием приложенного к ней момента сил , то совершаемая при этом работа равна:

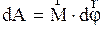. (2.3.10)

Формула (2.3.10) получается из (2.3.8), если учесть (2.2.6) и (2.2.36). Мощность N равна работе, совершаемой в единицу времени:

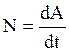. (2.3.11)

Взяв dA в виде (2.3.8) и (2.3.10), получим для мощности два выражения

, . (2.3.12)

Механическая энергия системы частиц есть мера механического движения ее. Полная механическая энергия системы и потенциальной энергии:

E=W+П. (2.3.13)

Кинетическая энергия системы N частиц W есть сумма кинетических энергий всех частиц системы: 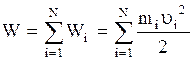. (2.3.14)

Если система движется поступательно, то скорости всех частиц одинаковы, тогда , (2.3.15)

где m - масса системы частиц. Если система частиц вращается вокруг неподвижной оси, то угловая скорость всех частиц одинакова и подставляя (2.2.14), (2.2.31), (2.3.4) в (2.3.14), получим

, (2.3.16)

где - момент инерции системы частиц относительно той же оси. Если система частиц движется поступательно и вращается вокруг некоторой оси, то ее кинетическая энергия: W=W_пост+W_вращ.

Потенциальная энергия системы частиц П есть энергия, зависящая от взаимного расположения взаимодействующих консервативными силами частиц внутри системы и взаимного расположения данной системы частиц и других систем частиц, которые взаимодействуют друг с другом консервативными силами. Соответственно этому выделяют потенциальную энергию внутреннего взаимодействия частиц в системе П_внутр и потенциальную энергию внешнего взаимодействия частиц в системе П_внутр и потенциальную энергию внешнего взаимодействия данной системы частиц с другими П_внеш, а полная потенциальная энергия системы частиц есть их сумма:

П=П_внутр +П_внеш.. (2.3.17)

Все общефизические законы справедливы и при описании механического движения системы частиц, хотя имеют некоторые особенности.

1. Принцип инерции /первый закон Ньютона/ для системы частиц гласит: в инерциальной системе отсчета скорость центра инерции изолированной системы частиц остается неизменной.

2. Принцип относительности имеет тот же вид, что и для одной частицы: законы изменения состояния физических систем не зависит от того, к какой из инерциальных систем отсчета относятся эти изменения.

3. Постулат Эйнштейна: скорость света в вакууме одинакова по всем направлениям, не зависит от скорости движения источников и приемников света и является максимально возможной скоростью в природе.

4. Кинематические уравнения для системы частиц, движущейся поступательно и вращательно в общем случае имеют вид:

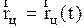(2.3.18)

и 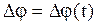, (2.3.19)

где 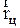- радиус-вектор центра инерции системы частиц, 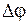- угол поворота системы частиц относительно оси вращения. Для конкретных случаев движения эти уравнения имеют определенный вид.

Так, при равнопеременном поступательном движении системы частиц уравнения движения имеют вид:

(2.3.20)

и 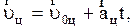(2.3.21)

где 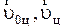- начальная и конечная скорости движения центра инерции системы частиц, - ускорение центра инерции. Если в качестве системы частиц выбрать абсолютно твердое тело, то при его поступательном движении скорости и ускорения всех частиц тела одинакова и уравнения (2.3.21) справедливы для любой частицы твердого тела. При вращательном движении системы частиц с постоянным угловым ускорением вокруг некоторой оси уравнения в проекциях на эту ось имеют вид:

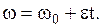(2.3.22)

5. К общефизическим законам справедливым для механического движения системы частиц относится и закон сохранения импульса системы частиц, являющийся следствием однородности пространства. Этот закон гласит: Полный импульс изолированной системы частиц в инерциальной системе отсчета остается неизменным, хотя импульсы частиц системы могут изменяться,

P=const. (2.3.23)

Для неизолированной системы частиц не изменяются проекции полного импульса системы на те направления, по которым взаимодействие отсутствует, или векторная сумма действующих сил равна нулю.

6. Силы, действующие на систему частиц, подчиняются принципу независимости поэтому их можно складывать векторно в равнодействующую

. (2.3.24)

7. Если на систему частиц действует сила то полный импульс системы изменяется, подчиняясь второму закону Ньютона:

(2.3.25)

Другой вид этого закона получается, если (2.3.25) умножить на dt. Тогда

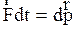, (2.3.26.)

т.е. импульс силы, действующей на систему частиц равен изменению полного импульса системы. Подставляя (2.3.3) в (2.3.25) и используя (2.3.1), получим для случая неизменной массы системы второй закон Ньютона в третьей формулировке: . (2.3.27)

8. Взаимодействие системы частиц с внешними частицами или с другими системами частиц является взаимным и подчиняется в механике третьему закону Ньютона, который в формулировке самого Ньютона, переведенной акад. А. Н. Крыловым гласит: ” Действию всегда есть равное и противоположное противодействие”.

9. Для механического движения системы частиц существенны лишь гравитационное и электромагнитное взаимодействия из четырех видов фундаментальных взаимодействий. Гравитационное взаимодействие систем частиц, как и гравитационное взаимодействие отдельных частиц подчиняется закону всемирного тяготения. Для нахождения сил тяготения двух систем нужно найти силы тяготения между каждой частицей 1-й системы и каждой частицей 2-й системы по (2.2.60), а затем определить равнодействующую всех сил притяжения частиц 1-й системы и равнодействующую сил притяжения частиц 2-й системы. Эти равнодействующие и будут силами гравитационного взаимодействия двух систем частиц.

10. Электромагнитное взаимодействие при механическом движении систем частиц оценивается силами упругости и силами трения. Как известно из курса физики средней школы, силы упругости вводят для описания контактного взаимодействия системы частиц, сопровождающегося деформацией. В случае, когда в качестве систем частиц взяты два контактирующих абсолютно твердых тела (рис. 2.3.3), деформация тел равна нулю, а взаимодействие их описывается силами: 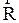- реакции опоры, - нормального давления. Если система частиц подвержена упругой деформации, например, пружина растягивается деформирующей силой F_деф, (рис. 2.3.4) то как установлено экспериментально Гуком, сила упругости пропорциональна удлинению пружины 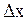и направлена в сторону противоположную смещению частиц пружины и деформирующей силе:

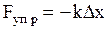. (2.3.28)

Рис. 2.3.3

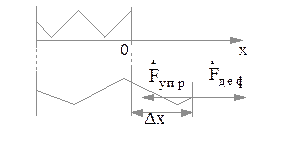
Рис. 2.3.4

Утверждение (2.3.28) называют законом Гука.

11. Силы трения вводят для описания взаимодействия соприкасающихся систем частиц при перемещении их или частей одной системы относительно друг друга. Трение между поверхностями абсолютно твердых тел называется внешним, а трение между слоями жидкостей или газов называется внутренними. Внешнее трение подчиняется приближенно опытному закону Амонтона, согласно которому максимальная сила трения покоя, сила трения скольжения, сила трения качения не зависят от площади соприкосновения тел и пропорциональны силе нормального давления, прижимающей трущиеся поверхности друг другу 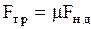, (2.3.29)

где m - коэффициент трения, зависит от природы и состояния соприкасающихся поверхностей. Внутреннее трение подчиняется другим законам, которые будут рассмотрены в теме, посвященной описанию механического движения жидкостей и газов.

12. К общефизическим законам относится и закон сохранения момента импульса системы частиц, являющийся следствием изотропности пространства. Этот закон гласит: полный момент импульса изолированной системы частиц в инерциальной системе отсчета остается постоянным, хотя моменты импульса частиц внутри системы могут изменяться:

. (2.3.30)

Для неизолированной системы частиц не изменяются проекции полного момента импульса системы на те направления, по которым взаимодействие отсутствует, или векторная сумма моментов сил, действующих на систему, равна нулю.

13. Если данная система частиц взаимодействует с другими, то ее момент импульса изменяется, подчиняясь уравнению моментов для системы частиц:

. (2.3.31)

Согласно (2.3.31) производная по времени от полного момента импульса системы частиц относительно начала системы отсчета равна векторной сумме моментов внешних сил относительной той же точки. Если (2.3.31) спроектировать на неподвижные оси прямоугольной системы координат, то получим эквивалентные равенства

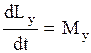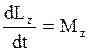; ; . (2.3.32)

Эти соотношения называют уравнениями моментов относительно соответствующих неподвижных осей.

Применяя (2.3.32) к вращательному движению абсолютно твердого тела относительно некоторой неподвижной оси и учитывая (2.3.3), (2.2.34), (2.2.26) получим: или, если =const, то

, (2.3.33)

которое называют основным законом динамики вращательного движения вокруг неподвижной оси: произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси. Если (2.3.31) умножить на dt, то получим еще одну формулировку этого закона: , (2.3.34)

согласно которой изменение момента импульса системы частиц равно импульсу момента сил, действующих на систему частиц.

14. К общефизическим законам относится и закон сохранения энергии, являющейся следствием однородности времени. Этот закон для механического движения системы частиц гласит: механическая энергия изолированной системы частиц в инерциальной системе отсчета не изменяется, если частицы внутри системы не взаимодействуют или взаимодействуют консервативными силами

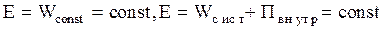, (2.3.35)

где - кинетическая энергия поступательного и вращательного движения системы, 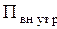- потенциальная энергия взаимодействия частиц внутри системы. Е - полная механическая энергия системы частиц в инерциальной системе отсчета сохраняется, если как внутреннее, так и внешнее взаимодействие осуществляется консервативными силами:

, (2.3.36)

где - потенциальная энергия взаимодействия данной системы частиц с другими системами. Если же взаимодействие частиц внутри системы или внешнее взаимодействие системы осуществляется неконсервативными силами, то механическая энергия системы частиц изменяется, причем изменение механической энергии системы равно работе неконсервативных сил :

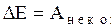. (2.3.37)

Дата добавления: 2014-11-16