
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
С большими скоростями
|
|
|
|
Применение механических представлений к описанию движений
2.5.1. Кинематические представления релятивистской механики
Для описания движения с большой скоростью (сравнимой с максимальной равной с = 3 108 м/с). Эйнштейн в 1905 г. создал релятивистскую механику, называемую также специальной теорией относительности, если движение рассматривается в инерциальной системе отсчета. Обобщенная на случай неинерциальной системы отсчета, она называется общей теорией относительности и является современной теорией тяготения.
Основу специальной теории относительности составляют два постулата, принцип относительности и принцип постоянства скорости света содержание которых уже обсуждалось. Из этих постулатов следует ряд выводов, касающихся свойств пространства и времени, поэтому эту теорию называют также физическим учением о пространстве и времени. в ней впервые свойства пространства и времени рассматривались тесно связанными между собой и с законами физических явлений, совершающихся в ней.
Связь пространства и времени особенно наглядна в тех преобразованиях координат и времени, с помощью которых можно перейти от одной инерциальной системы отсчета к другой. Ранее обсуждалось, что все инерциальные системы отсчета равноправны из - за однородности и изотропности пространства - времени. отличаться друг от друга инерциальные системы отсчета могут либо а) сдвигом начала системы отсчета, б) поворотом координатных осей, в). либо сдвигом начала отсчета времени, либо г) относительным равномерным и прямолинейным движением. В последнем случае существенно влияние численного значения скорости движения, именно его рассмотрим подробно.
Пусть имеем две инерциальные системы отсчета, которые обозначим О и О’ рис. 2.5.1, причем система О’, движется относительно системы О с большой
постоянной скоростью 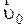 .
.
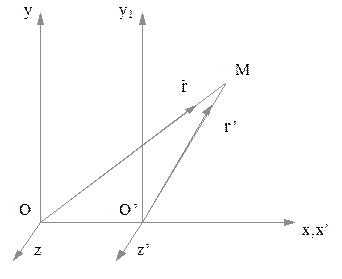
Рис. 2.5.1
Направим оси 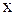 и
и 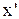 вдоль вектора скорости
вдоль вектора скорости 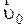 , а оси
, а оси 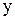 и
и 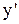
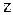 и
и 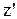 параллельно друг другу. Будем считать, что в начальный момент времени начала систем отсчета совпадали. Положение произвольной частицы М относительно системы О определяется
параллельно друг другу. Будем считать, что в начальный момент времени начала систем отсчета совпадали. Положение произвольной частицы М относительно системы О определяется 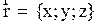 , а относительно O’
, а относительно O’ 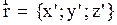 . Связь
. Связь 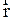 и
и 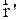 ,
, 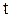 и
и 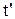 , а следовательно
, а следовательно 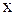 и
и 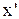 ,
, 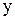 и
и 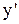 ,
, 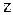 и
и 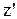 дается преобразованиями координат и времени Лоренца. Можно показать, что для рассматриваемого случая они имеют вид:
дается преобразованиями координат и времени Лоренца. Можно показать, что для рассматриваемого случая они имеют вид:
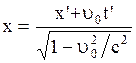 ;
; 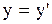 ;
; 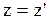 ;
; 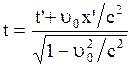 (2.5.1)
(2.5.1)
или 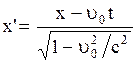 ;
; 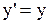 ;
; 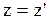 ;
; 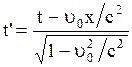 . (2.5.2)
. (2.5.2)
Для случая малых скоростей движения 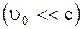 формулы (2.5.1) и (2.5.2) переходят в:
формулы (2.5.1) и (2.5.2) переходят в: 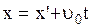 ;
; 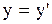 ;
; 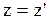 ;
; 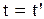 (2.5.3)
(2.5.3)
или  ;
; 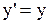 ;
; 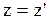 ;
; 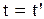 , (2.5.4)
, (2.5.4)
которые впервые были получены Галилеем, а потому называются преобразованиями координат и времени Галилея.
При 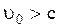 формулы (2.5.1) и (2.5.2) не имеют смысла. Это согласуется с принципом постоянства скорости света о невозможности движения в пустоте со сверхсветовыми скоростями.
формулы (2.5.1) и (2.5.2) не имеют смысла. Это согласуется с принципом постоянства скорости света о невозможности движения в пустоте со сверхсветовыми скоростями.
Рассмотрим следствия из преобразований Лоренца:
1). Необходимость введения для каждой системы отсчета собственного времени, поскольку течение времени зависит от скорости движения системы. Это непосредственно следует из вида преобразований Лоренца, согласно которым 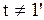 . Лишь в случае малых скоростей, как видно из преобразований Галилея,
. Лишь в случае малых скоростей, как видно из преобразований Галилея, 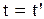 т.е. время одинаково течет во всех инерциальных системах отсчета.
т.е. время одинаково течет во всех инерциальных системах отсчета.
2). Относительность временного интервала, т.е. неодинаковость длительности событий в разных инерциальных системах, движущихся относительно друг друга с большой скоростью. Покажем, что длительность, например, горение лампы по часам быстро движущейся системы отсчета больше, чем по часам, которые покоятся по отношению к лампе. Пусть лампа, находящаяся в системе О (рис. 2.5.1) в точке с координатами 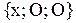 , включена в момент времени
, включена в момент времени 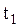 и выключена в
и выключена в 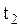 . Тогда
. Тогда
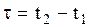 (2.5.4)
(2.5.4)
- длительность горения лампы по часам системы О. Длительность горения той же лампы по часам системы О’ равна
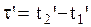 . (2.5.5)
. (2.5.5)
Выразим 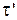 через
через 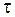 , для этого в (2.5.5) подставим выражение
, для этого в (2.5.5) подставим выражение 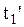 и
и 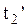 соответственно через
соответственно через 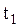 и
и 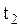 по (2.5.2), тогда получим:
по (2.5.2), тогда получим:
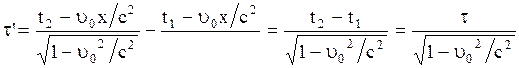 (2.5.6)
(2.5.6)
Получили, что 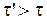 в
в 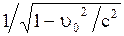 раз. Иными словами, длительность событий в различных системах различна, причем наименьшая длительность в этой системе, в которой событие происходит, а по отношению к другим инерциальным системам отсчета, движущимся со скоростью
раз. Иными словами, длительность событий в различных системах различна, причем наименьшая длительность в этой системе, в которой событие происходит, а по отношению к другим инерциальным системам отсчета, движущимся со скоростью 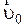 , длительность того же процесса больше и тем больше, чем ближе
, длительность того же процесса больше и тем больше, чем ближе 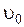 к
к 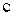 . Если
. Если 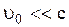 , то
, то 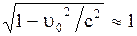 и
и 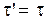 , т.е. длительность события в таких системах одинакова. Замедление времени экспериментально обнаружено у релятивистских элементарных частиц и используется в ускорителях для определенных целей.
, т.е. длительность события в таких системах одинакова. Замедление времени экспериментально обнаружено у релятивистских элементарных частиц и используется в ускорителях для определенных целей.
3). Относительность одновременности событий. Пусть в системе отсчета О рис. 2.5.1 в момент времени 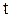 происходит одновременно два события в точках с координатами
происходит одновременно два события в точках с координатами 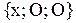 и
и 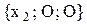 . Выясним, будут ли одновременными эти события с точки зрения системы О, движущейся по отношению к системе О с большой скоростью
. Выясним, будут ли одновременными эти события с точки зрения системы О, движущейся по отношению к системе О с большой скоростью 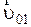 . В системе О этим событиям соответствует момент времени
. В системе О этим событиям соответствует момент времени 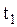 и
и 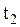 , которые связаны с
, которые связаны с 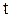 преобразованием по (2.5.2):
преобразованием по (2.5.2):
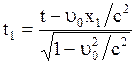 и
и 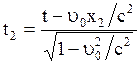 .
.
Найдем: 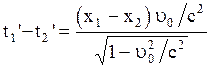 . (2.5.7)
. (2.5.7)
Из (2.5.7) видно, что момент времени 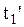 и
и 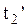 будут совпадать, т.е. события в О’ будут одновременными, если оба события происходят в одном и том же месте т.е.
будут совпадать, т.е. события в О’ будут одновременными, если оба события происходят в одном и том же месте т.е. 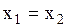 . Если
. Если 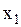 не равно
не равно 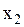 , то события в системе О’ не одновременны. Следовательно, понятие одновременности событий можно применять лишь к той системе, в которой они происходят, т.е. одновременность событий относительна. В случае малых скоростей движения системы О в (2.5.7)
, то события в системе О’ не одновременны. Следовательно, понятие одновременности событий можно применять лишь к той системе, в которой они происходят, т.е. одновременность событий относительна. В случае малых скоростей движения системы О в (2.5.7) 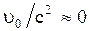 и
и 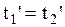 . Это означает, что события, одновременные в одной системе, будут одновременными и в других покоящихся или медленно движущихся системах.
. Это означает, что события, одновременные в одной системе, будут одновременными и в других покоящихся или медленно движущихся системах.
4). Относительность пространственного интервала, т.е. неодинаковость длины отрезков в различных инерциальных системах отсчета, движущихся относительно друг друга с большой скоростью. Покажем, например, что стержень длиной 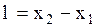 , (2.5.8)
, (2.5.8)
закрепленной в системе О будет иметь меньшую длину с точки зрения системы О’ (рис. 2.5.1). Обозначим длину этого стержня, измеренную в 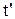 из системы О’ через
из системы О’ через 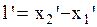 . (2.5.9)
. (2.5.9)
Из преобразований (2.5.1): 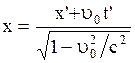 , отсюда
, отсюда
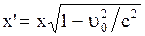 . (2.5.10)
. (2.5.10)
Подставим (2.5.10) в (2.5.9) получим:
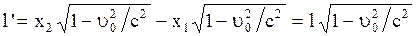 . (2.5.11)
. (2.5.11)
Из (2.5.11) видно, что 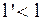 , т.е. длина отрезков в различных системах отсчета различна, причем наибольшая она в той системе, по отношению к которой он покоится, а в других системах, движущихся с большой скоростью, длина того же отрезка меньше и тем меньше, чем ближе
, т.е. длина отрезков в различных системах отсчета различна, причем наибольшая она в той системе, по отношению к которой он покоится, а в других системах, движущихся с большой скоростью, длина того же отрезка меньше и тем меньше, чем ближе 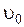 к
к 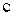 . Следует отметить, что сокращение длины происходит лишь в направлении движения, поперечные размеры не изменяются. Если же
. Следует отметить, что сокращение длины происходит лишь в направлении движения, поперечные размеры не изменяются. Если же 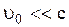 в (2.5.11)
в (2.5.11) 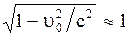 и
и 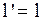 , т.е. длина отрезков в покоящихся или медленно движущихся относительно друг друга системах одинакова.
, т.е. длина отрезков в покоящихся или медленно движущихся относительно друг друга системах одинакова.
5). Инвариантность пространственно - временного интервала. Величины или соотношения называются инвариантными, относительно преобразований Лоренца (2.5.1), если они не изменяются при переходе от одной инерциальной системы отсчета к другой с использованием преобразований координат и времени Лоренца. К инвариантным величинам, например, относятся: скорость света в вакууме, собственное время системы. Одним из инвариантных выражений является пространственно - временной интервал, т.е. интервал между двумя событиями, происходящими в моменты времени 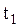 и
и 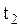 , промежуток между которыми равен
, промежуток между которыми равен  , пространственное расстояние между которыми равно
, пространственное расстояние между которыми равно 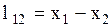 . Пространственно - временной интервал имеет вид:
. Пространственно - временной интервал имеет вид:
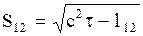 . (2.5.12)
. (2.5.12)
Подстановкой (2.5.1) в (2.5.12) можно убедиться, что в системе О’ пространственно - временной интервал будет иметь такой вид:
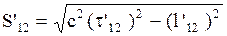 .
.
6). Релятивистское сложение скоростей. Если частица М (рис. 2.5.1) движется со скоростью 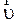 относительно системы О’ и
относительно системы О’ и 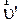 относительно системы О, а скорость системы О по отношению к системе О’ равна
относительно системы О, а скорость системы О по отношению к системе О’ равна 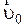 и сравнима с
и сравнима с 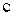 , то правило векторного сложения этих скоростей
, то правило векторного сложения этих скоростей 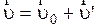 которым пользуются в механике малых скоростей, оказывается не выполняющимся. В рассматриваемом случае скорости связаны более сложными соотношениями. Так, для случая одинакового направления вдоль оси х скоростей
которым пользуются в механике малых скоростей, оказывается не выполняющимся. В рассматриваемом случае скорости связаны более сложными соотношениями. Так, для случая одинакового направления вдоль оси х скоростей 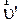 и
и 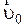 , можно получить формулу:
, можно получить формулу: 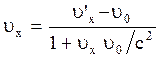 . (2.5.13)
. (2.5.13)
Если скорости 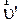 и
и 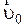 малые, то (2.5.13) переходит в известную:
малые, то (2.5.13) переходит в известную: 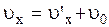 . Соотношение (2.5.13) никогда не приводит к скоростям, превышающим скорость света. Даже, если
. Соотношение (2.5.13) никогда не приводит к скоростям, превышающим скорость света. Даже, если 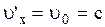 (2.5.13):
(2.5.13): 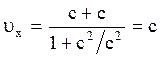 . Это связано с тем, что в основе преобразований Лоренца и его следствий лежит принцип постоянства скорости света.
. Это связано с тем, что в основе преобразований Лоренца и его следствий лежит принцип постоянства скорости света.
7). Можно сказать, что ускорение частицы в различных движущихся относительно друг друга с большими скоростями инерциальных системах отсчета не одинаковы, т.е. не инвариантны.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 506; Нарушение авторских прав?; Мы поможем в написании вашей работы!