Описание затухающих колебаний

В реальных колебательных системах всегда существует сопротивление движению, что приводит к потере части энергии колебаний, иначе говоря, к диссипации энергии и затуханию колебаний.

Рассмотрим затухающие колебания осциллятора - шара, подвешенного на невесомой пружине (рис. 2.6.1), помещенного в вязкую среду, которая оказывает сопротивление, пропорциональное скорости

, (2.6.32)

где - коэффициент сопротивления. Тогда на шар кроме упругой силы и силы тяжести будет действовать 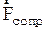и уравнение второго закона Ньютона в проекции на ось 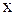с учетом (2.6.1) будет иметь вид

. (2.6.33)

Зная, что 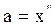, , 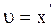вводя обозначение , , 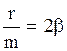подставляя их в (2.6.33), получим дифференциальное уравнение затухающих колебаний

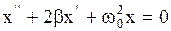. (2.6.34)

Как известно из курса высшей математики, при , то есть при небольшом затухании решение (2.6.34) имеет вид:

, (2.6.35)

где 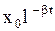-можно рассматривать амплитуду затухающего колебания, убывающую со временем. График, соответствующий (2.6.35) изображен на рис. 2.6.6.

Рис. 2.6.6

Величина - есть циклическая частота, тогда период затухающего колебания равен 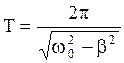. (2.6.36)

Из этой формулы следует, что с увеличением 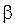период растет, а при , T oбращается в бесконечность. В последнем случае никаких колебаний не возникает. Система, выведенная из расстояния равновесия, возвращается в него, не совершая колебаний. Такой процесс называется периодическим. В рассматриваемой системе он возможен, если вязкость среды, в которую помещен шар, велика, так что . Величину 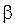называют коэффициентом затухания. Он прямо пропорционален коэффициенту сопротивления и обратно пропорционален массе осциллятора. Введем величину - время релаксации 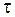- время, за которое амплитуда колебания уменьшается в 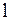раз. Тогда по определению 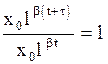или откуда . Следовательно, коэффициент затухания обратен времени релаксации, т.е. 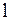времени, за которое амплитуда колебаний уменьшается в раз.

Еще одной характеристикой затухающего колебания является логарифмический декремент затухания , который равен натуральному логарифму отношения амплитуд, соответствующих моментам времени, отличающимся на период. Согласно определению

, (2.6.37)

где есть число колебаний, совершаемых за время релаксации, за которое амплитуда колебаний убывает в 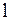раз. Из (2.6.37)следует, что логарифмический декремент затухания обратен числу колебаний, совершаемых за время релаксации.

Итак, если на осциллятор, кроме квазиупругой силы, действует сила сопротивления, пропорциональная скорости, то осциллятор совершает приближенно гармонические колебания, амплитуда которых экспоненциально убывает со временем, круговая частота тем меньше, чем больше коэффициент затухания. Для получения незатухающих колебаний осциллятора необходимо восполнение убыли энергии, т.е. необходимо действие вынуждающей силы, работа которой затрачивается на преодоление сопротивления. В таком случае колебания осциллятора называют вынужденными.

Дата добавления: 2014-11-16