Движения в системе частиц с упругими связями

Применение механических представлений к описанию волнового

Волны представляют собой процесс распространения колебаний в пространстве. Различают волны звуковые, электромагнитные, волны на поверхности жидкости и др. Несмотря на различную физическую природу, волны любого типа имеют много общего и подчиняются аналогичным закономерностям.

Будем рассматривать механические или упругие волны, которые могут распространяться лишь в системе частиц, обладающей упругими свойствами. Такую систему частиц называют сплошной упругой средой, непрерывно распределенной в пространстве. Частицей среды считают малый элемент ее объема, размеры которого в тоже время во много раз больше межмолекулярных расстояний.

Если какую - либо частицу среды заставить колебаться, то она приведем в колебательное движение упруго связанные с ней соседние частицы. При этом возникают периодические деформации в упругой среде, которые будут передаваться от одних частиц к другим, вовлекая в колебательный процесс все более удаленные от источника колебаний частицы среды. В зависимости от характера, возникающих при этом упругих деформаций, различают волны продольные и поперечные. Волна называется продольной, если направление колебания частиц среды совпадает с направлением распространения колебаний. Волна называется поперечной, если направление колебаний частиц среды перпендикулярно направлению распространения колебаний в упругой среде. Продольная волна представляет собой чередование сгущений и разряжений в упругой среде, возникающих при деформациях расширения - сжатия, поэтому они возникают в тех средах, в которых возможны подобные деформации, т.е. в газах, жидкостях, твердых телах. Поперечная волна возможна лишь в среде, где деформация сдвига вызывает упругие силы, т.е. в твердых телах. Волны на поверхности жидкости под воздействием сил земного притяжения и сил поверхностного натяжения движутся более сложным образом.

Поверхность, которая отделяет колеблющиеся частицы от частиц, еще не пришедших в колебательное движение называется фронтом волны. Совокупность точек, колеблющихся в одинаковых фазах, образует волновую поверхность. Фронт волны представляет собой одну из волновых поверхностей. Если фронт волны есть плоскость, волна называется плоской, если фронт волны имеет форму сферы, волна называется сферической. Рассмотрим уравнение простейшего типа в волны - гармонических, когда источник колебаний совершает гармонические колебания. Поскольку при этом частота колебания определенная, то волна распространяющаяся от источника и обладающая той же частотой, называется монохроматической. Пусть волна распространяется по упругой среде только в одном положительном направлении от х т.е. является плоской.

Поместим источник колебаний в начало системы отсчета О. Уравнение колебаний источника: , где 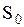, , 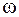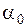- соответственно амплитуда, круговая частота и начальная фаза колебаний. Пусть скорость распространения волны равна 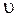. Тогда чем дальше отстоит рассматриваемая частица среды от источника, тем позже она начинает колебаться. Время запаздывания колебания равно 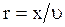, где 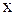- координаты рассматриваемой частицы среды, а фаза равна 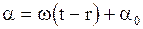. Следовательно, уравнение колебаний произвольной частицы среды имеет вид:

(2.7.1)

- есть уравнение плоской монохроматической гармонической волны. В (2.7.1) колеблющаяся величина зависит от двух переменных 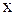и 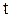. Графическое изображение волны возможно, если одна из переменных зафиксирована, например, 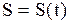для частицы среды с координато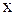й или 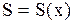для момента времени (рис. 2.7.1. а, б).

Соотношение (2.7.1) является решением дифференциального уравнения:

, (2.7.2)

которое называют волновым уравнением. Убедиться в этом можно прямой подстановкой (2.7.1) в (2.7.2). Под можно понимать различные величины, так при упругих волнах это могут быть и смещение частицы среды, и ее скорость, и ее ускорение, а в случае электромагнитных волн - вектор индукции магнитного поля или вектор напряженности электрического поля. Вообще, если какая-нибудь физическая величина зависит от времени и координат так, что ее частные производные удовлетворяют уравнению (2.7.2), то величина распространяется в виде плоской волны. На рис. 2.7.1.б изображены смещения в некоторый момент времени 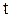различных частиц среды в волновом процессе. Видно, что фазы колебания частиц различны.

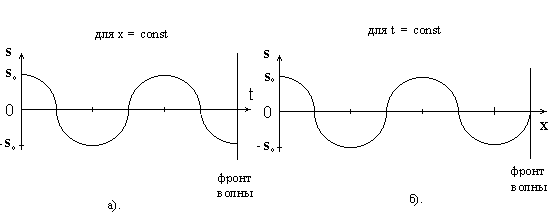
Рис. 2.7.1

Расстояние между двумя ближайшими частицами, колеблющимися в одинаковых фазах, называется длиной волны. За время, равное одному периоду колебания, волна распространится на расстояние равное длине волны, поэтому

, (2.7.3)

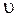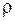где - скорость распространения волны, которую называют фазовой скоростью, т.к. она характеризует скорость перемещения фазы колебания. В общем случае, значения фазовой скорости зависит от природы волн, от частоты колебаний и свойств той среды, в которой распространяется волна. Так, например, скорость поперечных волн в твердых телах равна , где - модуль сдвига, - плотность твердого тела, скорость продольных волн в твердых телах равна , где 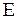- модуль упругости, 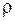- плотность твердого тела. Зависимость скорости распространения волны от частоты называется дисперсией. Вид этой зависимости различен для разных волн. Для упругих гармонических волн дисперсия равна нулю, т.е. фазовая скорость не зависит от частоты колебаний, а электромагнитные волны обладают дисперсией. Согласно (2.7.3) длина волны зависит как от периода колебаний источника, так и от свойств среды, в которой распространяется волновой процесс. Следует отметить, что частота волны не является инвариантной величиной, т.е. при переходе из одной инерциальной системы отсчета в другую, инерциальную движущуюся относительно первой, частота изменяется. Это явление называется эффектом Доплера, который наблюдается для всех волн любой природы, например, и для упругих, и для электромагнитных. Можно показать, что для упругих волн с уменьшением расстояния между источником и приемником воспринимаемая приемником частота больше частоты источника; при увеличении расстояния между источником и приемником воспринимаемая приемником частота меньше частоты волн источника. Для электромагнитных волн связь частот источника и приемника более сложная. Эффект Доплера применяют для изменения частоты волны с изменением скорости излучается, приближая ее к собственным частотам колеблющихся систем, и добиваясь резонанса, при котором осциллятор поглощает энергию волны, что обнаруживается приборами, и позволяет оценить собственную частоту и другие параметры осциллятора. Это особенно важно, если осцилляторами являются атомы, ядра или отдельные элементарные частицы. Такие методы исследования называются резонансными. Любая система, в которой происходят колебания, обладает повышенным запасом энергии по сравнению с невозбужденным состоянием этой системы, поскольку, чтобы возбудить колебания в источнике колебаний, к нему нужно подвести энергию извне. При распространении волны энергия передается тем частицам среды, которые начинают колебаться, т.е. волны переносят энергию. Определим изменение энергии малого объема 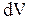упругой среды, в которой распространяется плоская монохроматическая гармоническая волна (2.7.1). Полная механическая энергия этого объема равна сумме его кинетической и потенциальной энергии деформации: 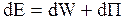, (2.7.4)

причем , (2.7.5)

где - масса 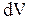, 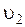- скорость колебания частиц, которую для всех частиц будем считать одинаковой и равной

. (2.7.6)

Массу малого объема выразим через плотность Среды

. (2.7.7)

Подставляя (2.7.6) и (2.7.7) в (2.7.5), получим для кинетической энергии объема 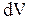среды: . (2.7.8)

Можно показать, что потенциальная энергия объема 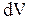в случае распространения в среде как продольной, так и поперечной волны равна его кинетической энергии, т.е.

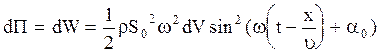. (2.7.9)

Тогда полная механическая энергия объема 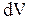равна:

. (2.7.10)

Объемная плотность энергии волн в упругой среде равна:

. (2.7.11)

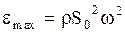. (2.7.12)

Сравнивая (2.7.8 - 2.7.10) с (2.6.19, 2.6.21, 2.6.23), следует отметить, что кинетическая и потенциальная энергии некоторого объема среды, по которой проходит волна, меняются в одной фазе, т.е. одновременно достигают максимума и минимума. В противоположность этому, кинетическая и потенциальная энергии отдельной гармонически колеблющейся частицы меняются в противофазе, т.е. при максимуме кинетической энергии потенциальная минимальна и наоборот. Кроме того, полная механическая энергия гармонически колеблющейся изолированной частицы с течением времени остается неизменной, а полная механическая энергия участка среды, в которой распространяется волна, изменяется со временем по (2.7.10), т.е. энергия из одного участка переходит в другие, вовлекаемые в волновой процесс. Как следует из (2.7.12) максимальная энергия единицы объема среды прямо пропорциональна квадрату амплитуды, квадрату частоты и плотности cреды.

Если в среде распространяются одновременно несколько монохроматических гармонических волн, то согласно принципу суперпозиции результирующее колебание каждой частицы среды есть геометрическая сумма колебательных процессов наложившихся волн. Принцип суперпозиции (независимости) выполняется только для волн, описываемых линейными дифференциальными уравнениями типа (2.7.2). Для упругих волн (2.7.2) справедливо, если деформация среды в процессе волнового движения малы и подчиняются закону Гука (2.3.28). При сложении нескольких волн могут возникнуть некоторые особые эффекты, которые называются волновыми явлениями. Наиболее ярким эффектом сложения волн является интерференция, заключающаяся в создании в некоторой области пространства, устойчивой картины такого распределения энергии колебания, что места с максимальной амплитудой чередуются с местами минимальной амплитудой колебаний. Если источников колебания очень много, то подобное явление называют дифракцией. Интерференция и дифракция возникают, если складываются волны, имеющие разность фаз, не изменяющиеся со временем, для монохроматических волн это требование сводится к условию равенства частот складывающихся волн. Если складываются волновые процессы разных, но близких частот, то согласно (2.6.49) возникают биения, т.е. приближенно гармонический колебательный процесс, амплитуда которого изменяется периодически со временем, то увеличиваясь, то уменьшаясь. Если такой процесс распространяется в пространстве, то оказывается возможным следить за перемещением максимума биения, который называют волновым пакетом или группой волн (рис. 2.7.2).

В виде группы волн с близкими частотами можно представить любую не гармоническую волну, какой является всякая реальная волна. Если скорость 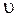распространения волны не зависит от частоты, т.е. нет дисперсии, то скорости всех складывающихся волн одинаковы и, следовательно, скорость движения волнового пакета также равна 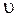. При этом движение не изменяем форму пакета. Если скорость 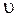зависит от частоты, то скорости распространения складывающихся волн различны, хотя и близки по значению, как частоты. Тогда под

Рис. 2.7.2

скоростью движения пакета понимают скорость передвижения в пространстве максимума пакета. Эту скорость называют групповой. Групповая скорость может быть как меньше, так и больше фазовой скорости максимума пакета. Следует отметить, что из-за различия скоростей распространения отдельных волн пакета форма изменяется со временем, пакет как бы расплывается.

Глава 3. Основы статистической физики и термодинамики

Дата добавления: 2014-11-16