
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинетическим, потенциальным, полным энергиям
|
|
|
|
Распределение Максвелла и Больцмана молекул газа по скоростям,
Если газ находится в состоянии равновесия, молекулы движутся беспорядочно, хаотически. Все направления движения равновероятны. Скорости молекул могут быть самыми различными. При каждом столкновении скорости молекул изменяются, причем могут возрасти и уменьшиться, но очень малые и очень большие по сравнению со средним значением скорости маловероятны. При каждой определенной температуре распределение молекул по скоростям определенное, при котором скорости молекул группируются вблизи наиболее вероятного значения скорости для данной температуры. Распределение молекул газа по скоростям теоретически рассчитал Максвелл (1859 г). Он рассматривал систему из молекул в равновесном состоянии, в которой
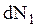 молекул имеют скорости от
молекул имеют скорости от 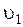 до
до 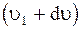 ,
,
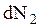 молекул имеют скорости от
молекул имеют скорости от 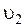 до
до 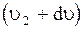 ,
,
 молекул имеют скорости от
молекул имеют скорости от 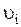 до
до 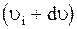 ,
,
тогда объем области значений от 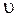 до
до 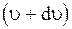 равен
равен 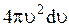 , следовательно число молекул, скорости которых от
, следовательно число молекул, скорости которых от 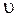 до
до 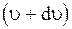 равен:
равен:
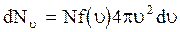 . (3.19)
. (3.19)
Вероятность того, что скорость молекулы окажется в интервале от 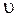 до
до 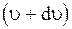 равна
равна 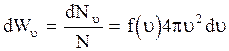 . (3.20)
. (3.20)
Отношение 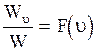 называется функцией распределения молекул по скоростям. Максвелл рассчитал, что
называется функцией распределения молекул по скоростям. Максвелл рассчитал, что 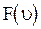 имеет вид:
имеет вид:
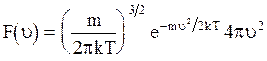 , (3.21)
, (3.21)
где 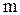 - масса молекулы,
- масса молекулы, 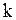 - постоянная Больцмана,
- постоянная Больцмана, 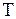 - абсолютная температура. График функции
- абсолютная температура. График функции 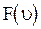 изображен на рис. 3.1. Площадь под каждой кривой равна единице, т.е. функция распределения
изображен на рис. 3.1. Площадь под каждой кривой равна единице, т.е. функция распределения 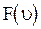 нормирована на единицу:
нормирована на единицу:
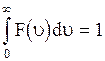 .
.
Зная функцию распределения, можно найти среднее значение скорости молекул: 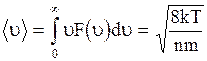 (3.22)
(3.22)
- среднеарифметическая скорость;
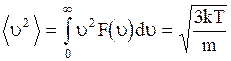 (3.23)
(3.23)
- среднеквадратичная скорость. Максимумы кривых распределения соответствуют наиболее вероятной скорости 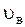 которая связана с температурой соотношением:
которая связана с температурой соотношением: 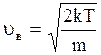 . (3.24)
. (3.24)
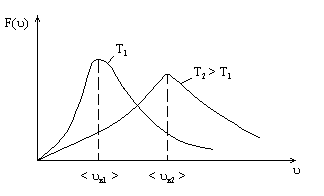
Рис. 3.3
Сравнивая (3.22), (3.23), (3.24), получим:  .С повышением температуры максимум кривой распределения смещается вправо и становится ниже. Функция распределения зависит также от массы молекул, причем для молекул с большей массой функция распределения имеет более острый максимум, сдвинутый влево.
.С повышением температуры максимум кривой распределения смещается вправо и становится ниже. Функция распределения зависит также от массы молекул, причем для молекул с большей массой функция распределения имеет более острый максимум, сдвинутый влево.
Экспериментально распределения Максвелла было проверено впервые качественно Штерном в 1920 г, а позднее в других опытах оно подтвердилось и количественно.
В показателе экспоненты в (3.21) стоит выражение 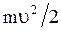 , которое представляет собой кинетическую энергию молекулы, движущейся со скоростью
, которое представляет собой кинетическую энергию молекулы, движущейся со скоростью 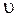 . Поэтому распределение максвелла по скоростям можно представить как распределение молекул по их кинетическим энергиям.
. Поэтому распределение максвелла по скоростям можно представить как распределение молекул по их кинетическим энергиям.
Соответствующая функция распределения будет иметь вид:
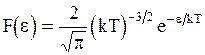 . (3.25)
. (3.25)
Больцман (1866 г) установил функцию распределения молекул идеального газа, находящегося в потенциальном поле сил тяжести, а позже обобщил ее на случай распределения большого числа любых одинаковых макрочастиц, находящихся в любом потенциальном поле
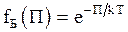 , (3.26)
, (3.26)
где  - потенциальная энергия одной частицы.
- потенциальная энергия одной частицы.
Распределения максвелла по кинетическим энергиям и Больцмана по потенциальным энергиям можно объединить в распределение частиц по их полным энергиям 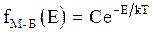 (3.27)
(3.27)
- есть функция распределения Максвелла - Больцмана для системы макрочастиц, находящихся во внешнем потенциальном поле.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 504; Нарушение авторских прав?; Мы поможем в написании вашей работы!