Фундаментальные представления термодинамики

Термодинамика изучает состояния и процессы изменения состояния макросистем, не рассматривая микроскопического строения систем, а исходя из основных термодинамических законов, являющихся обобщением опытных данных. В настоящее время такой подход широко применяется для исследования самых различных физических и химических процессов, свойств макросистем. 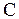Наиболее важными величинами, используемыми в термодинамике, являются количество тепла, , теплоемкость , работа 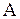в термодинамических процессах, давление, объем, температура, внутренняя энергия, энтропия состояния системы.

Процесс называют термодинамическим, если изменяются хотя бы один макропараметр системы. Среди термодинамических процессов различают равновесные и неравновесные процессы. Процесс называется равновесным, если представляет собой последовательность равновесных состояний макросистемы. Поскольку в равновесном состоянии значения каждого макропараметра во всех частях системы одинаково, то равновесное состояние системы изображается на графиках , и других точкой, а равновесный процесс - кривой. Неравновесное состояние характеризуется разными значениями макропараметров для различных частей системы. Неравновесный процесс это процесс, при котором хотя бы одно из промежуточных состояний неравновесно. Неравновесные состояния и процессы графически изобразить невозможно. Реальные процессы являются неравновесными и могут считаться равновесными с большей или меньшей точностью. Среди равновесных процессов выделяют изопроцессы, в которых один из макропараметров остается неизменным. Так, процесс, происходящий при постоянном объеме называют изохорическим, при постоянном давлении - изобарическим, при постоянной температуре - изотермическим. Важным является адиабатический процесс, происходящий без теплообмена системы с окружающей средой. Работа и количество тепла являются различными способами изменения внутренней энергии и передачи ее от одной системы к другой. Поэтому, если внутренняя энергия есть среднее значение полной энергии частиц, составляющих систему, и характеризует состояние системы, то теплота и работа характеризуют изменение состояния системы, т.е. происходящие процессы и являются функциями термодинамических процессов. 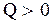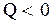Принять считать , , если система получает количество тепла, и , , если система отдает теплоту; , 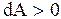если исследуемая система совершает работу над другими системами, и , , 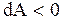если работа совершается над исследуемой системой.

Найдем выражение для работы, совершаемой системой (рис. 3.4) в каком - либо термодинамическом процессе, при котором объем системы увеличивается, например, газ расширяется.

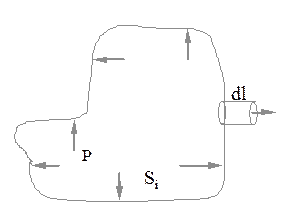
Рис. 3.4

Пусть состояние системы равновесно и давление в системе равно 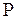, причем по определению , где - малая часть площади поверхности системы. Если при расширении системы каждая площадка сместилась на , то при этом совершена элементарная работа

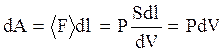. (3.28)

Работа по расширению всей системы равна:

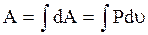. (3.29)

По формуле (3.29) определяется работа в любом равновесном термодинамическом процессе.

Для описания тепловых свойств систем в термодинамике вводят такую величину как теплоемкость. Теплоемкостью 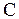системы в данном термодинамическом процессе называется отношение количества тепла 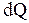, переданного системе в процессе к изменению температуры 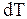, происшедшему при этом:

. (3.30)

Из определения следует, что теплоемкость, как количества тепла и работа, есть функция процесса. Теплоемкость одного моля системы называют молярной теплоемкостью , равной количеству тепла, которое нужно сообщить одному молю системы в данном термодинамическом процессе, чтобы изменить температуру его на один кельвин. Согласно определению:

. (3.31)

Теплоемкость единицы массы системы называют удельной теплоемкостью, равной количеству тепла, сообщенного единице массы системы в данном термодинамическом процессе для изменения температуры ее на один кельвин, т.е.

. (3.32)

Сравнивая (3.31) и (3.32), получим связь между молярной и удельной теплоемкостями для одного и того же процесса: 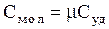. Перейдем к рассмотрению энтропии, введенной в термодинамику впервые Р. Клаузиусом в 1862 г. Существует два определения энтропии макроскопическое и микроскопическое. Согласно макроскопическому определению энтропия есть такая функция системы, элементарное изменение изменение которой при равновесном процессе равно полученному или отданному системой количеству теплоты, деленному на температуру, при которой произошел этот процесс:

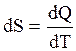(3.33)

или 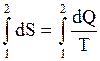, (3.34)

Формулы (3.33) и (3.34) позволяют рассчитывать не саму энтропию, а ее изменение, причем лишь для равновесных процессов, например, для адиабатического, для изопроцессов. Во всех случаях, когда системе сообщается некоторое количество тепла, т.е. 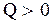, то 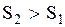и энтропия системы увеличивается, если система отдает некоторое количество тепла, т.е. 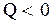, то , следовательно, энтропия системы уменьшается. Поскольку в адиабатическом процессе 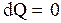, то 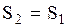, и адиабатический процесс может быть назван изоэнтропийным, т.е. происходящим при постоянной энтропии. Энтропия состояния системы определяется с точностью до произвольной постоянной. Из (3.34) следует: , т.е. энтропия в конечном состоянии равновесного процесса равна сумме энтропии начального состояния и интеграла не зависящего от формы кривой, изображающей рассматриваемый процесс, а определяющегося только начальным и конечным состояниями, т.е. пределами интегрирования.

Согласно микроскопическому определению, предложенному Больцманом, энтропия макросостояния системы прямо пропорциональна натуральному логарифму статистического веса этого макросостояния, т.е. прямо пропорциональна натуральному логарифму числа микросостояния, которыми данное макросостояние может быть получено:

, (3.3.5)

где 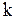- постоянная Больцмана, - статистический вес макросостояния. (3.35) как и (3.34) определяет энтропию с точностью до произвольной. Из (3.35) следует также что энтропия есть аддитивная величина, т.е. энтропия системы равна сумме энтропий всех частей системы. Поскольку статистический вес прямо пропорционален вероятности макросостояния, то и энтропия пропорциональна вероятности. Термодинамика основывается на трех опытных законах, называемых иногда началами термодинамики. Первый закон (начало) термодинамики справедлив для любых термодинамических процессов и является выражением закона сохранения энергии для термодинамических процессов. Этот закон гласит: количество тепла сообщаемое макросистеме, идет на приращение внутренней энергии и совершение системой работы над другими системами:

(3.36)

или в дифференциальной форме:

. (3.37)

Второй закон термодинамики - определяет направление термодинамических процессов. Исторически открытие второго закона связано с изучением вопроса о максимальном коэффициенте полезного действия тепловых машин, проведенным французским ученым Сади Карно. Позднее Клаузиус, Томсон, Больцман предложили различные по виду, но эквивалентные формулировки второго закона термодинамики. Согласно формулировке Клаузиуса, теплота не может самопроизвольно переходить от систем с более низкой температурой к системе с более высокой температурой. После введения понятия энтропии второй закон термодинамики стал формулироваться в виде: энтропия замкнутой системы при любых происходящих в ней процессах растет (если процесс неравновесный), либо остается постоянной (если процесс равновесный):

. (3.38)

Было показано, что всякий неравновесный процесс приводит систему в конце концов в равновесное состояние, в котором энтропия достигает максимума и никакие макропроцессы в такой системе невозможны. Изменение энтропии является количественной характеристикой степени необратимости процесса. Согласно (3.35) энтропия есть возрастающая функция статистического веса, поэтому при необратимых процессах статистический вес макросостояний изолированной системы возрастает. Поскольку статистический вес, а следовательно, и энтропия пропорциональны вероятности макросостояния, то переход в состояние с большим статистическим весом является и более вероятным, и равновесное состояние является наиболее вероятным. В связи с этим Больцман сформулировал второй закон термодинамики так: конечное состояние изолированной системы всегда имеет большую или ту же вероятность, что и начальное состояние. При этом если процесс равновесный, то вероятность состояний не изменяется, а если процесс неравновесный, то вероятность конечного состояния выше, чем у начального. Поскольку все реальные процессы неравновесные, то можно сказать, что природа стремится от состояний менее вероятных к состояниям более вероятным. В отличие от первого закона термодинамики, выполняющегося абсолютно, второй закон термодинамики имеет статистический характер и выполняется величина флуктуаций любого макропараметра, поэтому для системы из достаточно большого числа частиц (например, порядка числа Авогадро) флуктуациями вообще можно пренебречь. Именно для таких систем справедлив второй закон термодинамики.

С другой стороны, нельзя применять второй закон термодинамики к незамкнутым системам, например, к безграничной Вселенной, как это пытались делать некоторые физики. Так, Клаузиус, распространив действие второго закона на Вселенную, пришел к выводу о том, что со временем Вселенная переходя к равновесному состоянию, приобретет максимум энтропии и никакие необратимые процессы станут невозможными в ней, температура, концентрация, давление во Вселенной выравниваются. Такое состояние системы называют “тепловой смертью”. Утверждая возможность тепловой смерти Вселенной, Клаузиус должен признать, что когда - то и кем - то был дан “толчок извне” к сотворению мира, т.е. неизбежно становится на идеалистические позиции. Теория Клаузиуса была подвергнута критики Больцманом, позже Смолуховским и другими физиками, которые подчеркнули, что второй закон термодинамики применим лишь к изолированным системам, а безграничная Вселенная не может быть отнесена к изолированным системам.

В 1906 г Нернст сформулировал утверждение, получившее название третьего закона термодинамики. При абсолютном нуле температуры внутренняя энергия системы распределена между частицами, входящими в нее единственным образом: электроны в атомах находятся на наиболее низких энергетических уровнях, а атомы расположены в узлах кристаллической решетки твердого тела. Это состояние полностью упорядочено и его статистический вес равен единице. Поэтому энтропия согласно (3.35) равна:

, (3.39)

т.е. при абсолютном нуле температуры энтропия системы равна нулю - это и есть формулировка третьего закона термодинамики.

Дата добавления: 2014-11-16