И связь между ними. Уравнение равновесного состояния системы

Макроскопические параметры теплового движения частиц системы

Движения частиц в макросистемах

Применение представлений статистической физики к описанию теплового

Тепловым движением называется беспорядочное хаотическое движение частиц, составляющих макроскопические системы: газы, жидкости, твердые тела. Интенсивность теплового движения определяет состояние макросистемы, описываемое значениями макроскопических параметров. Макропараметры характеризуют состояние всей системы в целом, определяя общие тенденции в поведении очень большого числа частиц оценивая усредненную картину их движения. Макропараметры вычисляются как средние значения макропараметров, описывающих движения отдельных частиц макросистемы, по законам математической теории вероятности. Наиболее важными макропараметрами являются давление 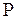, и температура 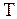, внутренняя энергия 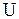, плотность 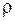. Наиболее важными микропараметрами являются: масса частицы, 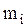, скорость 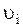, кинетическая энергия 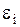, число частиц .

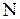Состояние макросистемы называется равновесным, если ее макропараметры для всей системы одинаковы и не зависят от времени. Свойства равновесного состояния не зависят от деталей движения отдельных частиц и определяются поведением всего коллектива частиц поэтому теряет смысл определение точного вида закона движения каждой частицы. Установившийся характер равновесного состояния проявляется в постоянстве во времени макропараметров. Флуктуация значений макропараметров в равновесном состоянии очень малы. Закон, выражающий зависимость между макропараметрами называются уравнением состояния макросистемы:

. (3.8)

Установление вида функции 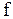, т.е. уравнение состояния, на основе представлений об атомном строении вещества и статистическом характере движения частиц в веществе является чрезвычайно сложной задачей, точно решенной только для самой простой модели - для идеального газа.

Газ называется идеальным, если удовлетворяет условиям:

1. частицы - молекулы, не имеют собственного объема, т.е. являются материальными точками,

2. молекулы друг с другом на расстоянии не взаимодействуют,

3. столкновение молекул абсолютно упругие,

4. хаотическое движение каждой молекулы подчиняется законам механики Ньютона.

Уравнение состояния идеального газа имеет вид:

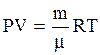, (3.9)

где 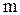масса газа, молекулярная масса его, 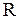= 8.31 Дж/(мольК) молярная газовая постоянная. При условиях близких к нормальным идеальными можно считать многие газы: кислород, водород, азот и другие. Для простых газов сложность строения молекул учитывают введением числа степеней свободы молекул . Если молекула содержит один атом, то ее число степеней свободы равно трем, как и для одной материальной точки, которая может двигаться только поступательно. Если молекула идеального газа содержит два атома, то 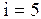, т.к. кроме поступательного возможны вращения такой молекулы вокруг взаимноперпендикулярных направлений. Если молекула идеального газа состоит из трех атомов, то . Газы с более сложным строением молекул менее похожи на идеальные.

Важным законом установленным для идеальных газов является закон равнораспределения энергии молекулы по степеням свободы, согласно которому на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная 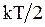называемая тепловой энергией. 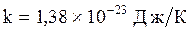и называется постоянной Больцмана. Следовательно, среднее значение кинетической энергии одной молекулы тем больше, чем сложнее молекула, и определяется формулой

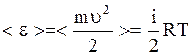. (3.10)

Здесь 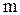- масса одной молекулы, 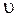- ее скорость. Формула (3.10) устанавливает связь макропараметра Т - температуры системы с микропараметром 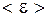- средней кинетической энергией отдельной молекулы и показывает, что температура характеризует интенсивность теплового движения частиц тела. В равновесном состоянии температура всей макросистемы одинакова. Если температура в разных частях макросистемы неодинакова, то происходит передача энергии от одних молекул другим. Механизм передачи энергии таков: там, где температура больше, частицы движутся быстрее; сталкиваясь с медленными, они передают им энергию; в результате быстрые частицы замедляются, а медленные начинают двигаться быстрее. Так происходит до тех пор, пока интенсивность хаотического движения в среднем, а следовательно, и температура не станут одинаковыми во всей макросистеме. При температуре абсолютного нуля 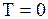, средняя кинетическая энергия молекулы идеального газа равна 0:

.

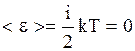В реальных газах с прекращением поступательного и вращательного движений молекул не прекращается колебательное движение молекул в положении равновесия. Не прекращаются и движения электронов внутри атомов. Так что и при абсолютном нуле нет абсолютного покоя. Поведение молекул при температурах близких к абсолютному нулю, обладает рядом существенных особенностей, поэтому оно не подчиняется законам для идеальных газов, а описывается квантовыми законами.

Сумма кинетической энергии движения всех частиц макросистемы и потенциальной энергии взаимодействия частиц друг с другом и с внешним полем составляет внутреннюю энергию макросистемы:

. (3.11)

Внутренняя энергия обладает свойством аддитивности, т.е. внутренняя энергия системы равна сумме внутренних энергий всех частей системы. Внутренняя энергия является функцией состояния макросистемы, т.е. зависит от макропараметров данного состояния. Вычислим внутреннюю энергию идеального газа объемом 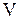, содержащем 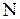молекул. Потенциальная энергия молекул идеального газа равна 0, т.к. молекулы идеального газа не взаимодействуют на расстоянии, следовательно внутренняя энергия идеального газа равна кинетической энергии всех молекул. Если считать, что все молекулы в равновесном состоянии обладают кинетической энергией близкой к среднему значению, то внутренняя энергия равна

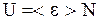. (3.12)

Общее число молекул 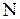можно выразить через число Авогадро 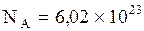1/моль и число молей газа в объеме 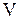равное 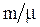, т.е.

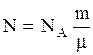. (3.13)

Подставляя (3.10), (3.13) в (3.12) и учитывая, что

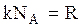, (3.14)

получим: 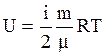. (3.15)

Используя уравнение состояния идеального газа Менделеева - Клапейрона (3.9), можно получить другое выражение для внутренней энергии идеального газа: . (3.16)

Со средней кинетической энергией отдельной молекулы связан и другой макропараметр - давление. По определению, давление есть абсолютное значение средней силы, действующей со стороны большого числа частиц газа или жидкости на каждую из поверхностей единичной площадки, помещенной в них. Давление обладает важным свойством: в жидкости или газе, не находящемся во внешнем поле, давление всегда одинаково во всех частях макросистемы, если состояние ее равновесно. Расчет давления идеального газа как средней силы, учитывающей суммарное действие молекул при соударениях с единичной площадкой, показал прямую пропорциональность давления средней кинетической энергии поступательного движения одной молекулы и числу молекул в единице объема идеального газа: , (3.17)

где (3.18)

есть число молекул в единице объема, т.е. плотность частиц или концентрации частиц. Формулу (3.17) называют основным уравнением молекулярно - кинетической теории, которая исторически послужила начальным этапом построения статистической физики, формулы (3.9) и (3.17) связаны между собой. Так если в (3.17) подставить (3.10), (3.13), (3.14), (3.18), то получим (3.9).

Дата добавления: 2014-11-16