Описание сложения гармонических колебаний

Характеристики колебаний

Вид колеба- ний Харак- теристика	Собственные	Затухающие	Вынужденные
Действующие силы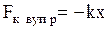
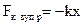
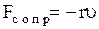
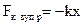
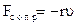
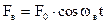
Дифференциальное уравнение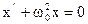
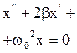
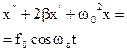
Уравнение колебаний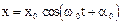
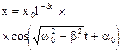
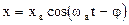
Амплитуда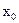
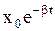
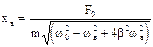
Круговая частота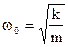
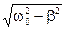
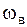
Период колебаний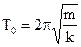

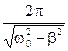
Если одна и та же частица участвует в нескольких колебаниях одновременно, то результирующее смещение частицы в каждый момент времени можно найти геометрически, сложив векторно смещения ее от каждого колебания в отдельности, поскольку для гармонических колебаний из - за линейности его дифференциального уравнения справедлив принцип суперпозиции.

Рассмотрим несколько частных случаев сложения колебаний.

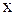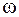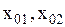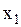1. Сложение двух одинаково направленных колебаний одинаковой частоты. Если два гармонических колебания происходят в одном направлении и имеют одинаковые частоты , но различные амплитуды и различные начальные фазы , то смещение и 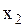для этих двух колебаний запишутся в виде:

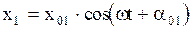и 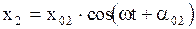. 2.6.45)

Результирующее смещение 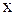, исходя из принципа суперпозиции, равно

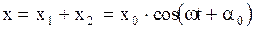, (2.6.46)

где 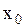- амплитуда, 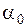- начальная фаза результирующего колебания. Для нахождения 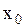и 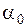воспользуемся методом векторных диаграмм. Зададим колебания 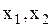соответствующими векторами 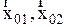(рис. 2.6.8).

Рис. 2.6.8

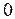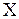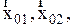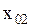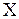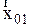Для этого из точки на горизонтальной оси проведем два вектора длина которых равна амплитудам и , а углы между векторами и осью равны соответственно - начальным фазам складываемых колебаний. Приведем во вращение векторы и 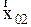против часовой стрелки с угловой скоростью равной циклической частоте колебаний. Тогда проекции векторов на ось Х будут изменяться гармонически со временем, подчиняясь уравнениям колебаний (2.6.45). Иными словами складываемые колебания 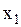и 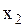представлены векторам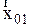и и 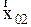, поэтому результирующее колебание может быть представлено вектором 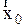, равным сумме векторов 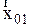и 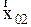: 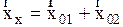. Построим по правилам сложения векторов результирующий вектор 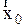, тогда проекция его на ось Х равна: 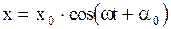, а с другой стороны: 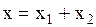. Из рис. 2.6.8 по теореме косинусов получим

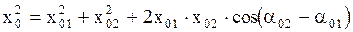(2.6.47)

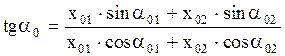. (2.6.48)

Поскольку скорость вращения векторов 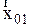и 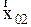одинакова, то угол между векторами все время остается постоянным, векторный треугольник не изменяет своей формы с течением времени, следовательно результирующий вектор 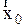вращается также со скоростью 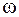, которой соответствует круговая частота результирующего колебания равная .

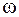Из (2.6.47) видно, что амплитуда 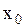зависит от разности начальных фаз складываемых колебаний. если разность фаз 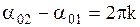, где 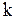- любое целое число, то 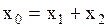и говорит, что колебания совпадают по фазе. Если 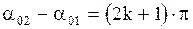, то 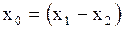, в этом случае колебания находятся в противофазах.

Таким образом, если частица одновременно участвует в двух или более колебаниях одинакового направления одинаковой частоты разных амплитуд и разных начальных фаз, то результирующее колебание будет того же направления, той же частоты, а амплитуда и начальная фаза определяются уравнениями (2.6.47) и (2.6.48).

Колебания одинакового направления, одинаковой частоты, с постоянной во времени разностью фаз называют когерентными. Как следует из рассмотренного примера, сложение когерентных колебаний может привести и к увеличению и к уменьшению результирующей амплитуды в зависимости от разности фаз складываемых колебаний.

Если складываются колебания одного направления, но разных частот, то в соответствующей векторной диаграмме колебаний векторы 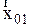и 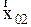вращаются с разными скоростями, поэтому угол между векторами изменяется со временем, и, следовательно, меняется со временем результирующий вектор, т.е. результирующее колебание не будет гармоническим.

В частном случае сложения колебаний одного направления, разных, но близких по значению частот, результирующее колебание можно считать гармоническим с периодически изменяющейся амплитудой и называется оно биениями.

Так, пусть складываются колебания 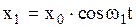и 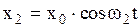причем амплитуды их равны между собой, начальные фазы равны нулю, а 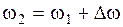, , 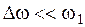то есть 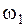и 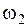близки по значению. Результирующее колебание

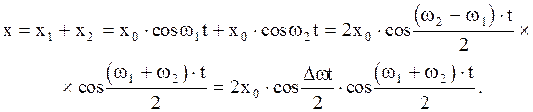(2.6.49)

Поскольку 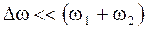, то множитель 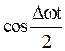изменяется со временем значительно медленнее, чем множитель 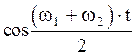, поэтому в (2.6.49) модуль выражения 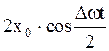можно рассматривать как амплитуду, причем частот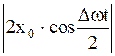а равна 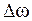, ее называют частотой биений. Следовательно, если частица одновременно участвует в двух колебаниях одинакового направления разных, но близких частот, то результирующим колебанием будет биение, амплитуда которого изменяется во времени с частотой равной разности частот складываемых колебаний, а частота результирующего колебания равна полу сумме частот складываемых колебаний. графически биения изображены на рис. 2.6.9. Биения представляют собой простейший пример модулированных колебаний, широко используемых в акустике и радиотехнике.

2. Сложение двух взаимно перпендикулярных колебаний.

Пусть частица участвует одновременно в двух колебаниях, направления которых взаимно перпендикулярны, причем одно колебание направлено по оси Х, другое - по оси 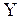. Пусть частоты складываемых колебаний одинаковы и равны 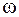, а амплитуды и начальные фазы разные. Тогда уравнение этих колебаний имеет вид: 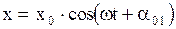и 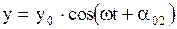. (2.6.50)

Рис. 2.6.9

Результирующее движение частицы согласно принципу суперпозиции равно векторной сумме колебаний, поэтому для нахождения уравнения траектории результирующего движения нужно исключить из уравнения (2.6.50) параметр 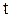. В результате этой операции получается следующее соотношение:

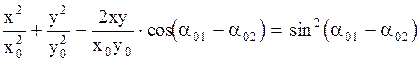. (2.6.51)

Из аналитической геометрии известно, что (2.6.51) определяет уравнение эллипса. Ориентация эллипса по отношению к координатным осям, а также величина осей эллипса зависит от амплитуд 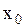и и 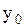разности фаз складываемых колебаний. Так, если разность фаз складываемых колебаний равна 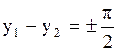, то уравнение (2.6.51) преобразуется в 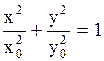, представляющим собой уравнение эллипса, приведенного к координатным осям, с полуосями равными амплитудам 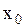и 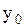(рис. 2.6.10).

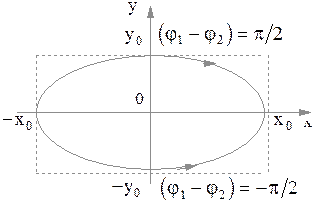
Рис. 2.6.10

Можно показать, что при 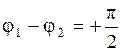частица движется по эллипсу по часовой стрелке, а при 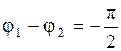против часовой стрелки. Если же разность фаз складываемых колебаний равна нулю, то уравнение (2.6.45) переходит в 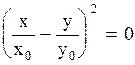или 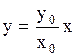, то есть частица движется по прямой, являющейся диагональю прямоугольника со сторонам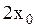и и 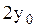(рис. 2.6.11).

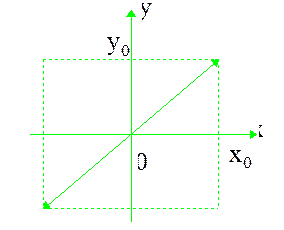
Рис. 2.6.11

В случае сложения взаимно перпендикулярных колебаний с разными частотами траектория результирующих колебаний более сложна. Их называют фигурами Лиссажу. Вид таких кривых зависит от соотношения амплитуд, частот начальных фаз складываемых колебаний. например при сложении двух взаимно-

Рис. 2.6.12

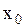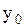перпендикулярных колебаний, у которых амплитуды равны и , разность

начальных фаз равна 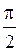, а отношение частот 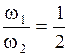, результирующая траектория имеет вид восьмерки, вписанной в прямоугольник со сторонам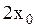и и 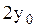(рис. 2.6.12).

Если же отношение частот равно при той же разности фаз 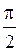, то результирующая кривая будет более сложной (рис. 2.6.13). Чем ближе к единице отношения частот складываемых колебаний, тем сложнее фигура Лиссажу.

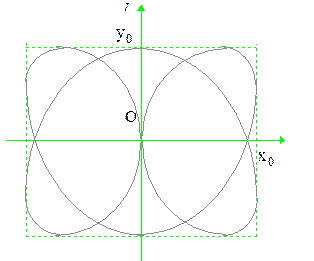
Рис. 2.6.13

Дата добавления: 2014-11-16