Колебательного движения

Применение механических представлений к описанию

2.6.1. Описание собственных колебаний

Особым видом движения является колебание.

Колебание - процесс, характеризующийся повторяемостью во времени значений физических величин, определяющих этот процесс. Колебания, в которых совершается механическое движение частицы или системы частиц, называют механическими. В механических колебаниях повторяются во времени значения координат, скоростей, ускорений и других связанных с ними величин.

В электрических колебаниях повторяются значения напряжения, сил токов, в электрических цепях, значения электрических и магнитных полей вокруг электрических цепей. Колебание называют периодическим, если значения изменяющихся величин повторяются через равные промежутки времени, а время одного полного колебания до начала его повторения есть период колебания Т.

Периодическое колебание называют гармоническим, если изменяющиеся зависят от времени по закону синуса или косинуса.

Многие в природе и техники близки к гармоническим или могут быть представлены как сложение нескольких гармонических колебаний.Поэтому подробнее рассмотрим именно гармоническое колебание.

Физические системы, совершающие гармонические колебания, называются гармоническими осцилляторами. Простейшим из механических осцилляторов является одна частица, совершающая гармонические колебания вдоль прямой. Например шар, подвешенный на невесомой пружине можно считать частицей, колеблющейся по вертикальному направлению.

В положении равновесия (рис. 2.6.1) сила тяжести 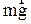уравновешивается упругой силой 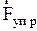, которая пропорциональна растяжению пружины 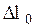поэтому шар покоится. В проекции на ось Х, второй закон Ньютона для этого случая имеет вид:

, (2.6.1)

где 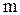- масса шара, 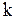- коэффициент жесткости пружины, 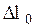- удлинение

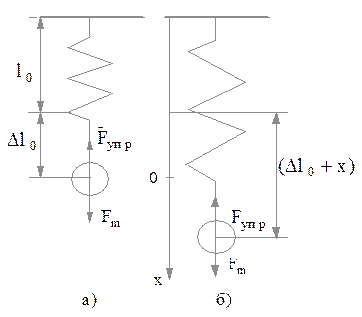
Рис. 2.6.1

пружины. При смещении шара вниз от положения равновесия в положение, характеризуемое координатой Х удлинение пружины составит 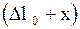(рис. 2.6.1.б), тогда уравнение второго закона Ньютона в проекции на ось Х для шара, имеет вид:

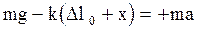. (2.6.2)

Подставив (2.6.1) в (2.6.2) получим:

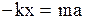. (2.6.3)

Вводя обозначение

, (2.6.4)

учтя, что

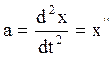, (2.6.5)

подставляя (2.6.4.) и (2.6.5.) в (2.6.3.),получим уравнение:

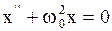, (2.6.6)

которое является дифференциальным уравнением колебания. Как известно из курса высшей математики, решение (2.6.6.) можно записать в виде:

. (2.6.7)

Уравнение(2.6.7.) есть уравнение гармонического колебания, в котором 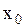- амплитуда, то есть максимальное смещение из положения равновесия, 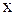-смещение в момент времени 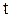, 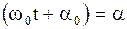- фаза колебания, характеризующая долю смещения в данный момент времени 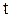от максимального смещения, 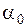- начальная фаза, 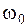- циклическая частота, равная числу колебаний, сделанных частицей за 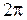секунд. Из (2.6.4.) видно, что

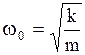, (2.6.8)

то есть зависит от параметров осциллятора, поэтому 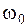называют собственной частотой осциллятора. 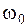связана с периодом колебания

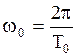. (2.6.9)

Подставляя (2.6.8) в (2.6.9) получим формулу для периода любых гармонических колебаний

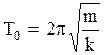. (2.6.10)

Зная выражение для смещения осциллятора в любой момент времени (2.6.7), можно получить зависимость скорости и ускорения его от времени:

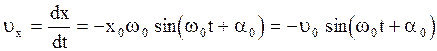, (2.6.11)

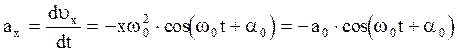. (2.6.12)

Сравнивая (2.6.7), (2.6.11), (2.6.12), следует отметить, что скорость колебания осциллятора смещена по фазе относительно 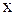на 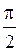, а ускорение изменяется со временем в противофазе по отношению к .

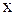Графики зависимости смещения, скорости, ускорения от времени изображены на рис. 2.6.2.

Обратим внимание на то, что в (2.6.3) проекция векторной суммы сил, действующих на шар, равна: 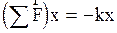, (2.6.13)

то есть пропорциональна смещению шара из положения равновесия, направлена к положению равновесия, как и для упругих сил. В связи с последним силы, неупругие по природе, но удовлетворяющие условию (2.6.13), называются квазиупругими. Осциллятор будет совершать гармонические колебания только,

если на него действуют упругая или квазиупругие силы, которые называют еще

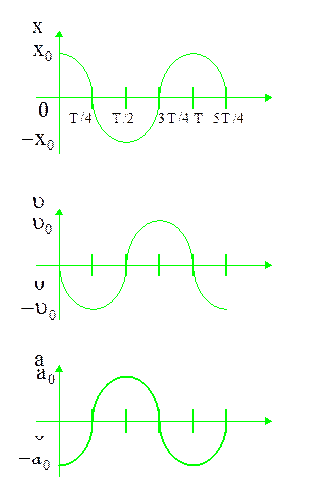
Рис. 2.6.2

возвращающими, поскольку направлены они всегда к положению равновесия осциллятора. Подставляя(2.6.7) в (2.6.13), получим

, (2.6.14)

то есть квазиупругая сила является примером силы, изменяющейся со временем гармонически. Наибольшее, или амплитудное, значение квазиупругой силы 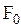равно: 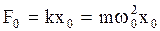. (2.6.15)

Подставляя (2.6.13) в (2.6.12), получим:

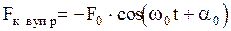. (2.6.16)

Вычислим работу квазиупругой силы по возвращению шара из положения с координатой 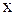в положение равновесия с координатой 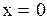. По определению работы (2.40) с учетом (2.6.13) получим .

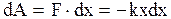Тогда 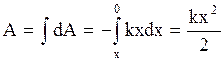. (2.6.17)

Используя связь работы квазиупругой, консервативной силы и убыли потенциальной энергии (2.5.1) и (2.6.17), можно найти потенциальную энергию осциллятора в положении с координатой :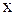

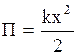(2.6.18)

или, с учетом (2.6.4) и (2.6.7),

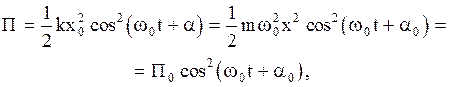(2.6.19)

где

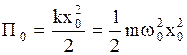(2.6.20)

- амплитудное значение кинетической энергии осциллятора. Используя формулу кинетической энергии частицы, движущейся с малой скоростью (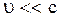) (2.4.8) и (2.6.11), получим выражение для кинетической энергии осциллятора:

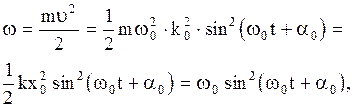(2.6.21)

где

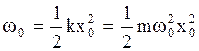(2.6.22)

- амплитудное значение кинетической энергии осциллятора. Полная механическая энергия осциллятора равна:

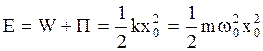. (2.6.23)

Следовательно, полная механическая энергия осциллятора остается постоянной во времени, пропорциональна массе, квадрату собственной частоты осциллятора, квадрату наибольшего смещения его из положения равновесия, т.е. равна амплитудным значениям кинетической и потенциальной энергии осциллятора. Из (2.6.19) и (2.6.21) следует, что при гармонических колебаниях кинетическая изменяется во времени 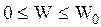превращаясь в потенциальную энергию, которая, в свою очередь, изменяется во времени 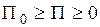, превращаясь в кинетическую, причем в каждый момент времени сумма кинетической и потенциальной энергий осциллятора одна и та же и определяется (2.6.23).

Построим график зависимости (рис. 2.6.3) потенциальной энергии осциллятора от его смущения из положения равновесия согласно (2.6.18). Такой вид зависимости 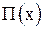называют потенциальной ямой. 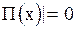. При этом осциллятор обладает наибольшим значением кинетической энергии 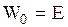. В состоянии с 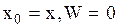, a .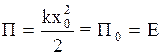

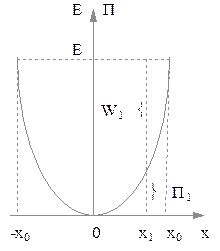
Рис. 2.6.3

Если смещение 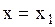, причем 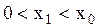, то энергия осциллятора равна 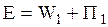. Значение полной энергии 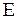ограничивает область допустимых смещений осциллятора 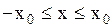. Можно показать, что колебания реальных систем будут гармоническими, если смещение системы из положения равновесия невелико, так что справедливо (2.6.18), тогда согласно (2.5)

.

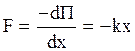Рассмотрим зависимость потенциальной энергии математического маятника от угла отклонения из его положения равновесия. Математическим маятником называют систему, состоящую из частицы массой 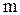, подвешенной на невесомой, нерастяжимой нити длиной 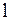в поле сил тяжести (рис. 2.6.4). Примем потенциальную энергию маятника в положении равновесия равной нулю, тогда при отклонении на угол 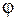потенциальная энергия маятника равна

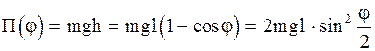. (2.6.24)

При малых 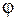можно принять 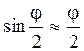, тогда

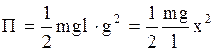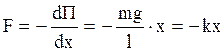, , где 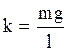(2.6.25)

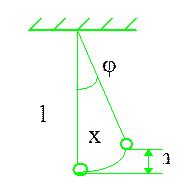
Рис. 2.6.4

Следовательно, математический маятник при малых углах отклонения совершает гармонические колебания, период которых с учетом (2.6.10) и (2.6.25) равен:

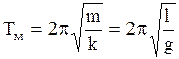. (2.6.26)

Такой же результат получился, если бы рассмотрели уравнение движения маятника. Получим уравнение колебания физического маятника. Физическим маятником называют систему частиц, которая может совершать колебания около оси, не проходящей через центр инерции системы. В качестве физического маятника выберем абсолютно твердое тело (рис. 2.6.5), подвешенное в точке О.

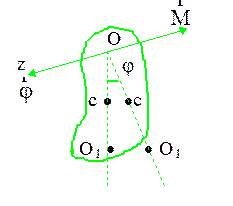
Рис. 2.6.5

Центр инерции тела в точке 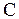, расстояние 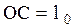. Если отклонить физический маятник от положения равновесия на угол j, то есть совершить угловое перемещение 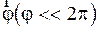, то возникает момент силы тяжести, стремящийся вернуть маятник в положение равновесия, причем 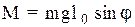, где 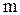- масса маятника 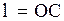. Согласно основному закону динамики вращательного движения, записанному в проекции на ось 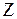, направленной как ,

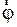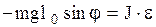, (2.6.27)

где 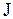- момент инерции маятника, 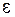- угловое ускорение, равное 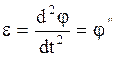. Рассмотрим малые отклонения, для которых 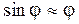, тогда (2.6.27) будет иметь вид:

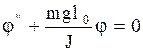. (2.6.28)

Обозначим

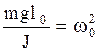, (2.6.29)

подставим в (2.6.28):

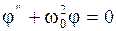. (2.6.30)

Полученное дифференциальное уравнение колебаний физического маятника идентично с (2.6.6). Его решение имеет вид:

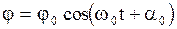
Следовательно, малые колебания физического маятника являются также гармоническими, причем период колебаний их с учетом (2.6.29) равен:

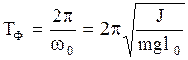. (2.6.31)

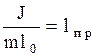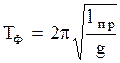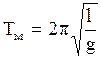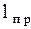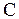Обозначим величину и подставим в (2.6.31), тогда вид формул и аналогичен, поэтому называют приведенной длиной физического маятника. Если на прямой, соединяющей точку подвеса с центром масс , отложить расстояние равное 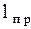от точки 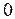, получим точку 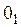, которую называют центром качания. Периоды колебания относительно 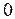и 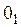одинаковы, поскольку 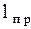одинакова в обоих случаях.

Дата добавления: 2014-11-16