Динамические представления в НСО

В НСО принцип инерции (первый закон Ньютона) не выполняется, это следует из (2.4.10), поскольку свободная частица, движущаяся относительно НСО с постоянной скоростью 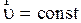, относительно ИСО будет иметь ускорение .

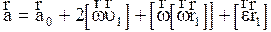В ИСО считается, что причиной ускорения является наличие взаимодействия, которые в механике описываются силами, причем по второму закону Ньютона:

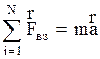, (2.4.14)

если на частицу действует N сил, каждая из которых обусловлена определенным взаимодействием. В НСО причиной появления дополнительных ускорений является неинерциальность системы, т.е. ее ускоренное поступательное и вращательное движение. Для учета неинерциальности системы отсчета в динамических законах, сформулированных в ИСО, вводят соответственно дополнительным ускорениям дополнительные силы, которые называют силами инерции. Для получения формул сил инерции умножим (2.4.11) на массу частицы m:

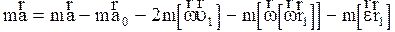, (2.4.15)

где 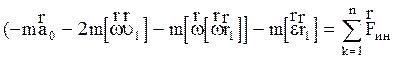, (2.4.16)

есть векторная сумма введенных сил инерции, подставив (2.4.14) и (2.4.16) в (2.4.15), получим второй закон Ньютона для НСО:

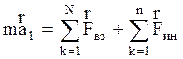, (2.4.17)

т.е. векторная сумма сил действующих на частицу и сил инерции равна произведению массы частицы на ее ускорение в НСО уравнение (2.2.56), (2.2.62) и (2.2.67) в НСО будут иметь вид:

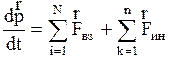, (2.4.18)

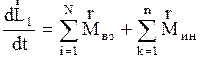, (2.4.19)

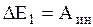. (2.4.20)

Законы сохранения импульса, момента импульса, механической энергии в НСО не выполняются, т.к. для свободной относительно НСО частицы выражения (2.4.18), (2.4.19), (2.4.20) имеет вид:

, , ,

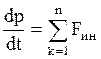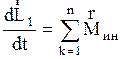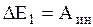следовательно импульс 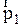, момент импульса 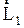, механическая энергия 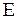частицы в НСО не остаются постоянными.

Из (2.4.16) видно, что силы инерции во всех случаях пропорциональны массе частицы m, так же, как и силы тяготения. Поэтому говорят об эквивалентности сил тяготения и сил инерции, положенной в основы общей теории относительности Эйнштейном.

2.4.3. Примеры описания движения в конкретных НСО

а). Пусть НСО движется относительно ИСО поступательно с ускорением 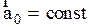. Частица М движется относительно НСО с ускорением 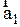. При этом 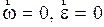. Тогда, учитывая (2.4.12) и (2.4.16), получим следующее выражение для сил инерции 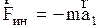. (2.4.21)

Так, если НСО имеет вид тележки, которая катится по горизонтальной поверхности, причем в тележке установлен кронштейн и подвешен на невесомой нерастяжимой нити шарик массой m (рис. 2.4.2), то 2-й закон Ньютона для НСО будет иметь вид

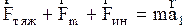, (2.4.22)

но шарик относительно НСО при установившемся движении остается в покое, т.е. 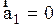и (2.4.22) принимает вид: 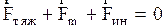, причем .

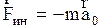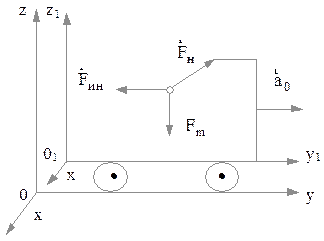
Рис. 2.4.2

б). Пусть НСО вращается относительно ИСО с постоянной угловой скоростью w, а частица М находится в покое, т.е. r₁ = a₁ = 0. В этом случае сила инерции равна

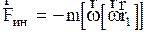. (2.4.23)

В качестве НСО выберем горизонтальную платформу, вращающуюся вокруг оси (рис. 2.4.3).

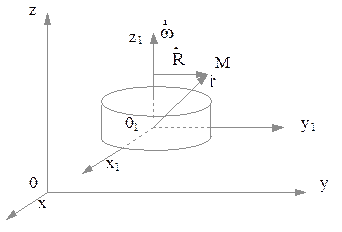
Рис. 2.4.3

Преобразуем выражение для ускорения в этом случае

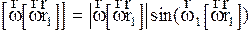, (2.4.24)

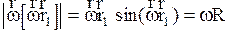, (2.4.25)

причем . Подставляя (2.4.25) и (2.4.26) в (2.4.24) получим:

. (2.4.26)

Направление двойного векторного произведения совпадает с направлением 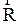. Отсюда 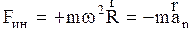. (2.4.27)

Такую силу инерции называют центробежной силой инерции 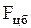, направлена эта сила от оси вращения по радиусу, против нормального ускорения. Во всех задачах о движении относительно вращающихся систем отсчета необходим учет центробежной силы инерции, например, при проектировании роторов турбин, электрических двигателей и других быстро вращающихся деталей. Действие центробежных сил инерции используется в центрифугах, сепараторах, центробежных насосах.

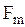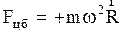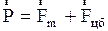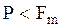Наша планета Земля является вращающейся системой отсчета, поэтому на каждое тело, находящееся на Земле, действует центробежная сила инерции. Так, на тело, лежащее на поверхности Земли, действует не только сила притяжения его к центру Земли , но и (рис. 2.4.4), тогда сила тяжести и . Например, для тела массой в 1 кг на экваторе .

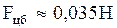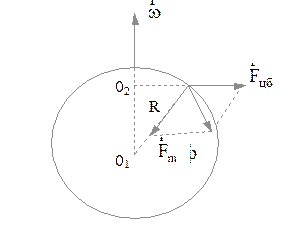
Рис. 2.4.4

в). Пусть НСО вращается относительно ИСО с постоянной угловой скоростью 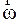, а частица М движется в НСО со скоростью 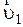. Исходя из (2.4.15) с учетом (2.4.27) в этом случае силы инерции имеют вид:

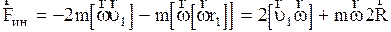. (2.4.28)

Силу инерции равную 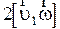называют силой Кориолиса и обозначают 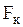, тогда 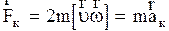, (2.4.29)

где 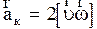- кориолисово ускорение. Направлена 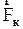перпендикулярно плоскости, в которой лежат 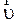и 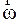, по правилу правого винта. Итак, на движущуюся с постоянной скоростью частицу во вращающейся системе отсчета действуют две силы инерции, при чем 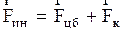. Проявление 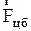и 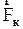можно наблюдать, если из центра вращающейся горизонтальной платформы заставить катится шарик. Под действием 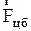шарик будет двигаться к краю платформы, однако траектории его движения не будет прямолинейной, т.к. действует 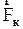, направленная как показано на рис. 2.4.5. в этом случае направлено перпендикулярно плоскости рисунка на нас.

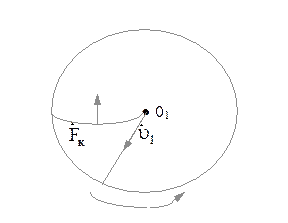
Рис. 2.4.5

На все движущиеся тела на Земле действует кроме центробежной силы инерции и силы Кориолиса, под влиянием которой изменяют свое направление ветры (пассаты), неодинаково изнашиваются рельсы при двухсторонней железной дорожной колее, подмываются течением рек определенные берега, отклоняются от прямоугольной траектории движущиеся снаряды, отклоняются от вертикали свободно падающие тела.

Дата добавления: 2014-11-16