Динамические величины для описания движения частицы

Законы механического движения одной частицы

Все общефизические законы, рассмотренные в главе 1, справедливы и при описании механического движения частицы и играют при этом существенную роль.

Напомним их формулировки.

1. Принцип инерции (1-й закон Ньютона): существуют системы отсчета, в которых свободная частица движется с постоянной скоростью, т.е. равномерно и прямолинейно.

Таблица 2.2.

Наименование величины	Обозначение и определение	Наименование величины	Обозначение и определение
масса	m	момент инерции
импульс		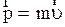момент импульса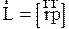
сила		момент силы
импульс силы		импульс момента силы
работа		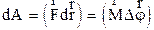мощность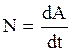
кинетическая энергия		потенциальная энергия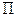
полная механическая энергия

2. Принцип относительности: во всех инерциальных системах отсчета законы физики имеют одинаковый вид.

3. Постулат Эйнштейна: скорость света в вакууме одинакова по всем направлениям, не зависит от скорости движения источников и приемников света и является максимально возможной скоростью в природе.

4. Кинематические уравнения для общего случая движения частицы имеют вид: или 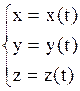и в угловых величинах: .

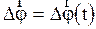Для частных случаев движения вид уравнения различен. Так, для равномерного движения частицы, т.е. при a = const и e =const, уравнения соответственно, в линейных и угловых величинах имеют вид:

(2.52)

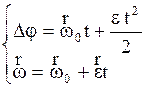, (2.53)

где 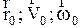- значение этих величин в начальный момент времени. Для гармонического колебания частицы уравнения движения имеют другой вид: 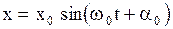. Скорость и ускорение при этом также зависят от времени.

5. К общефизическим законам, справедливым для механического движения, относится и закон сохранения импульса частицы, который является следствием однородности пространства. Этот закон гласит: импульс свободной частицы в инерциальной системе отсчета остается неизменным:

. (2.54)

Для несвободной частицы не изменяются лишь проекции импульса частицы на те направления, по которым взаимодействие отсутствует. Так, например, если частица притягивается Землей, то проекция её импульса на направление силы тяготения будет изменятся, а проекции её импульса на два других взаимоперпендикулярных направления будут оставаться неизменными.

6. Как уже говорилось выше, взаимодействие в механике оценивается силами. Опытным фактом является закон независимости действия сил: сила, с которой одна частица действует на другую, зависит лишь от радиус - векторов и скоростей этих двух частиц и не зависит от наличия взаимодействия с другими частицами. Отсюда следует, что все силы, действующие на данную частицу, можно складывать векторно в равнодействующую:

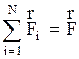. (2.55)

7. Если одна частица взаимодействует с другой, то импульсы их изменяются, причем изменение импульса в единицу времени оценивается действующей силой. Это утверждение составляет содержание одного из наиболее важных законов механики - второго закона Ньютона, который может быть записан в трех формулировках. Первая формулировка: в инерциальной системе отсчета производная от импульса частицы по времени равна равнодействующей сил, действующих на частицу, т.е. 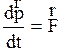. (2.56)

Умножив (2.56) на dt, получим другой вид второго закона Ньютона

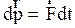, (2.57)

т.е. изменение импульса частицы в инерциальной системе отсчета равно импульсу равнодействующей сил, действующих на частицу. Третья формулировка второго закона Ньютона справедлива для случая постоянной массы частиц. Тогда, подставляя (2.32), (2.16) в (2.56), получим

. (2.58)

т.е. произведение массы частицы на её ускорение равно векторной сумме сил, действующих на частицу.

8. Всякое взаимодействие частиц является парным, т.е. если одна частица действует на другую, то и другая частица действует на первую. Взаимодействие приводящее к механическому движению, подчиняется третьему законы Ньютона: две частицы действуют друг на друга числено равными и противоположно направленными, т.е. 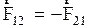. (2.59)

9. Из четырех видов фундаментальных взаимодействий, существующих в природе, при механическом движении существенны лишь гравитационное и электромагнитное. Гравитационное взаимодействие подчиняется закону всемирного тяготения, открытому Ньютоном в 1687 году: две частицы притягиваются друг к другу силами, пропорциональными произведению масс частиц, обратно пропорциональными квадрату расстояния между частицами и направленными по линии, соединяющей эти частицы. Так, на частицу массой m₁ (рис. 2.9) со стороны частицы массы m₂ действует сила тяготения

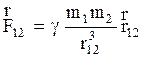, (2.60)

где - гравитационная постоянная, которая в Си равна.

Рис 2.9

Наибольшей силой притяжения из всех тел, окружающих нас, обладает Земля, поскольку ее масса наибольшая. Поэтому в физике чаще всего рассматривают гравитационное взаимодействие тел с Землей, а не между собой. Если поместить начало системы отсчета в центр Земли, а тело, которое можно считать при этом частицей массой m, на поверхность Земли, то модуль силы тяготения равен: F = g (m₃ m / R² ), где масса, R - радиус Земли. При этом g m₃ / R² = g - есть ускорение свободного падения, которое уменьшается с увеличением расстояния частицы от поверхности Земли и с перемещением её с полюсов на экватор Земли. Поле сил тяготения называют гравитационным полем. Гравитационное взаимодействие осуществляется с помощью обмена квантами гравитационного поля - гравитонами, которые экспериментально пока не обнаружены. Наличие электромагнитного взаимодействия при механическом движении учитывается введением упругих сил, сил трения, реакции опор, которые рассмотрим при описании законов механического движения систем частиц.

10. К общефизическим законам справедливым для механического движения относятся и закон сохранения момента импульса частицы, которой является следствием изотропности пространства. Этот закон гласит: момент импульса свободной частицы в инерциальной системе отсчета остается неизменным:

. (2.61)

Для несвободной частицы не изменяются проекции её момента импульса на те направления, по которым взаимодействие отсутствует.

11. Если одна частица взаимодействует с другой, то их моменты импульса изменяются, причем производная от момента импульса частицы по времени равна моменту силы действующей на частицу, т.е.

(2.62)

- это уравнение моментов для частицы. Если (2.62) умножив на dt, то получится вторая формулировка этого закона: , (2.63)

т.е. изменение момента импульса частицы равно импульсу момента силы, действующей на нее. Для случая неизменного момента инерции частицы подстановкой (2.34) и (2.26) в (2.62) получим третий вид этого закона:

, (2.64)

т.е. произведение момента инерции частицы на её угловое ускорение равно моменту силы, действующей на частицу.

12.К общефизическим законам справедливым для механического движения относятся и закон сохранения энергии, являющийся следствием однородности времени. Этот закон гласит: в инерциальной системе отсчета механическая энергия (кинетическая) свободной частицы остается неизменной, т.е.

. (2.65)

Механическая энергия частицы взаимодействующей с другими будет оставаться постоянной, если силы взаимодействия консервативны. Для этого случая

. (2.66)

Если взаимодействие происходит не консервативными силами, то механическая

энергия частицы меняется, причем изменение механической энергии частицы

равно работе неконсервативных сил:

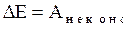. (2.67)

Таблица 2.3

Дата добавления: 2014-11-16