Динамические представления релятивистской механики

В механике малых скоростей импульс частицы по (2.2.32) равен 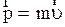. Если же скорость частицы 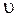сравнима со скоростью света, то связь импульса ее со скоростью иная: 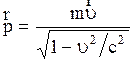, (2.5.14)

где 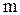масса частицы, не зависящая от скорости величина, одинаковая во всех инерциальных системах отсчета, т.е. инвариантная. При 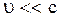выражение (2.5.14) переходит в (2.2.32). на рис. 2.5.2. показаны графики зависимостей импульса частицы при малых и больших скоростях движения. Как видно из рис. 2.5.2 различие между графиками становится значительным при приближении скорости частицы к скорости света.

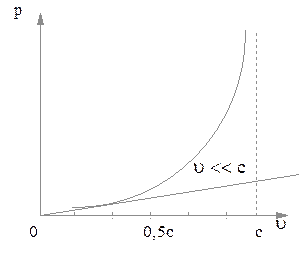
Рис. 2.5.2

В релятивистской механике справедлив закон сохранения импульса свободной частицы, т.е. 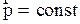, причем импульс частицы определяется (2.5.14). для несвободной частицы выполняется второй закон Ньютона в первой 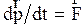и второй 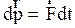формулировках, где 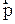- релятивистский импульс частицы (2.5.14). следует отметить, что импульс и сила представляют собой неинвариантные величины, т.е. переход из одной инерциальной системы отсчета в другую с помощью преобразований Лоренца дает разные значения 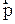и 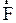. Для энергии свободной релятивистской частицы получено выражение:

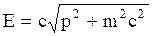, (2.5.15)

которое преобразуется в 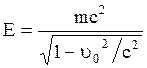, (2.5.16)

если вместо подставить его значение по (2.5.14). Если частица неподвижна, т.е. 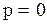, то по (2.5.15) энергия частицы равна

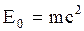(2.5.17)

и называется энергией покоя частицы, представляющую собой внутреннюю энергию, не связанную с движением частицы как целого. Из (2.5.16) и (2.5.17) можно выразит энергию движения, т.е. кинетическую энергию релятивистской частицы:

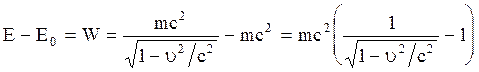. (2.5.18)

Для малых скоростей движения 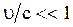, используя формулу разложения бинома Ньютона, согласно которой 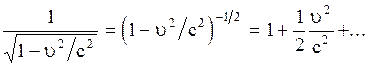и подставляя это выражение в (2.5.18), получим: 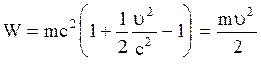, т.е. формулу кинетической энергии медленно движущейся частицы. Из (2.5.15. - 2.5.17) видно, что энергия и масса частицы взаимосвязаны, так что любое изменение энергии частицы повлечет за собой изменение ее массы и наоборот. В механике малых скоростей и макроскопических процессов рассматриваются такие изменения энергии, которые значительно меньше энергии покоя частицы и, следовательно, приводят к малым изменениям массы частиц, обычно не учитываемым.

В релятивистской механике и в микроскопических процессах возможны изменения энергии, сравнимые с энергией покоя частиц и превышающие ее, а поэтому необходимо учитывать изменение массы частиц, как это делается, например, при расчетах ядерных реакций, движении и превращениях элементарных частиц и других подобных случаях. Для релятивистской свободной частицы выполняется закон сохранения ее релятивистской энергии в форме (2.5.15) или (2.5.16). Если частица несвободна, находится в потенциальном поле и обладает потенциальной энергией П, то будет сохранятся суммарная энергия частицы поля.

Поскольку масса частицы и скорость света являются инвариантными величинами, то инвариантным будет выражение 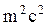. Но по (2.5.15)

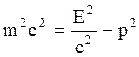, (2.5.19)

следовательно (2.5.18) - тоже инвариантное выражение относительно преобразований Лоренца. Из (2.5.15) следует возможность существования частиц с массой, равной нулю и энергией, равной

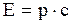. (2.5.20)

Приравнивая (2.5.16) и (2.5.19) и учитывая (2.5.14), получим, что для частиц с их скорость 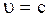. К таким частицам относятся фотоны, существующие только в движении со скоростью .

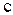Дата добавления: 2014-11-16