Описания вынужденных колебаний

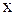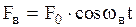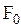Пусть на рассматриваемый осциллятор (рис. 2.6.1) действует по кроме квазиупругой силы, силы сопротивления, также вынуждающая сила, изменяющаяся со временем по гармоническому закону: , где - амплитудное значение, 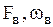- частота вынуждающей силы, тогда уравнение второго закона Ньютона в проекции на ось 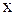будет иметь вид:

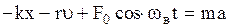. (2.6.38)

Введем обозначения: 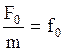, , , 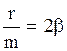подставим их в (2.6.38), зная, что 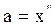, 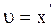. Тогда получим дифференциальное уравнение вынужденных колебаний осциллятора

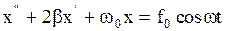. (2.6.39)

Уравнение (2.6.39) является неоднородным дифференциальным уравнением, поэтому его решение состоит из решения однородного уравнения (2.6.34) в виде (2.6.35) и частного решения неоднородного уравнения, соответствующего правой части (2.6.39). можно показать подстановкой в (2.6.39), что частное решение имеет вид: , (2.6.40)

где 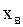- амплитуда вынужденного колебания, равная:

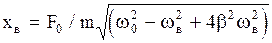, (2.6.41)

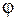- разность фаз смещения в вынужденных колебаниях и вынуждающей силы.

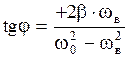. (2.6.42)

Решение (2.6.35) описывает затухающее колебание, поэтому через некоторое время им можно пренебречь, тогда решение (2.6.39) будет совпадать с частным решением (2.6.40) такие колебания называют установившимися вынужденными колебаниями, происходящими с частотой вынуждающей силы, с амплитудой и сдвигом фаз между смещением и вынуждающей силой, зависящими от этой частоты.

Исследуем зависимость амплитуды колебаний от частоты 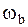вынуждающей

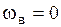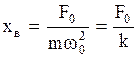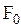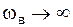силы (2.6.41) при амплитуда равна . Это есть смещение осциллятора из положения равновесия под действием постоянной внешней силы . При амплитуда уменьшается, то есть 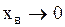. При некотором значении частоты амплитуда достигает максимума. Такая частота называется резонансной 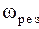, а явление возрастания амплитуды при приближении частоты вынуждающей силы к 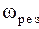- резонансом.

Для определения 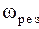нужно найти максимум функции (2.6.41). Продифференцировав подкоренное выражение по 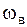и приравняв его к нулю, найдем

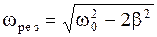. (2.6.43)

Подставив (2.6.43) в (2.6.41), получим выражение амплитуды при резонансе:

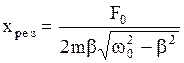. (2.6.44)

Из (2.6.44) видно, что чем меньше коэффициент затухания 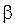, тем больше 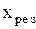, то есть тем острее максимум амплитуды при резонансе. Графически зависимость 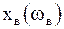называют резонансными кривыми. На рис. 2.6.7 изображены две резонансных кривых с разными коэффициентами затухания.

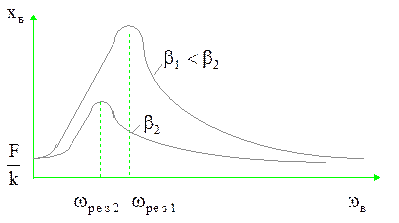
Рис. 2.6.7

Формула (2.6.42) дает возможность проанализировать изменение сдвига фазы 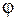между вынуждающей силой и смещением при вынужденных колебаниях.

При малых частотах 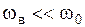значение 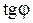мало, то есть смещение происходит практически синфазно с внешней силой. В области больших частот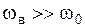 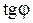стремится к нулю со стороны отрицательных значений, следовательно, сдвиг фаз равен 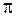и смещение осциллятора происходит в противофазе с вынуждающей силой. При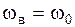 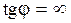, а 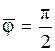. Если коэффициент затухания 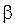мал, то можно считать 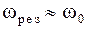, то есть в резонансе смещение отстает по фазе от внешней силы на 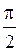. Явление резонанса находит широкое применение в научных исследованиях (в многочисленных резонансных методах изучения свойств веществ) и технике (радиотехнике, акустике). С другой стороны, возникновение резонанса стараются не допустить при создании машин, строительстве различных сооружений, подвергающихся периодическим воздействиям. Основные сведения по собственным, затухающим и вынужденным колебаниям сведены в таблице 2.6.1.

Таблица 2.6.1

Дата добавления: 2014-11-16