Тема 2: Двойной интеграл

2.1. Определение двойного интеграла

Если в определении кратного интеграла в качестве области 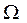взять плоскую область D, в которой определена функция двух переменных , то получим определение двойного интеграла:

(3)

где 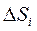- площадь 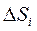участка разбиения области D.

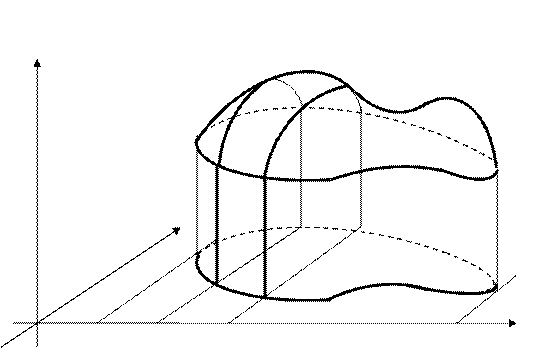
Для выяснения геометрического смысла двойного интеграла изобразим поверхность 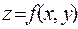в области D.

z

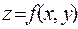
O y

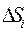
x

Из интегральной суммы (3) и приведенного рисунка следует, что если V - объём цилиндрического тела, ограниченного снизу областью D, а сверху – поверхностью , то .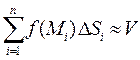

Переходя к пределу при 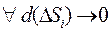, получим

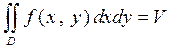. (4)

Таким образом, геометрический смысл двойного интеграла – объём цилиндрического тела, ограниченного снизу областью D, а сверху – поверхностью .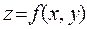

Замечание 2. Свойства двойного интеграла аналогичны свойствам кратного интеграла.

2.2. Вычисление двойного интеграла.

Определение 2. Правильной в направлении оси O у областью D называется область, удовлетворяющая следующим условиям:

1. Верхняя и нижняя её границы описываются уравнениям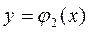и и 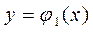соответственно;

2. Прямые 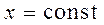пересекают её верхнюю и нижнюю границы не более чем в двух точках.

Аналогично определяется правильная область в направлении оси O x.

Формулу для вычисления двойного интеграла выведем, исходя из его геометрического смысла.

Пусть область D является правильной областью. Пересечем цилинд-рическое тело с нижним основанием – областью D, а верхним – поверх-ностью 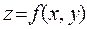, плоскостями x и :

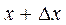z

y

O x

a x 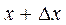b

Фиксируя x, вычислим интеграл 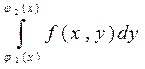, значение которого

равно площади криволинейной трапеции, полученной в сечении плоскостью 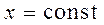. Если это выражение умножить на 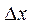и проинтегрировать от a до b, то из рисунка следует, что

,

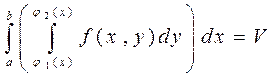где V - объём данной цилиндрической области.

Таким образом, получаем формулу для вычисления двойного интеграла

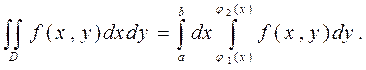(5)

Замечание 3. Если область правильная в направлении оси O x, то

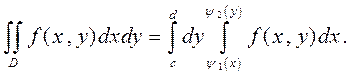(6)

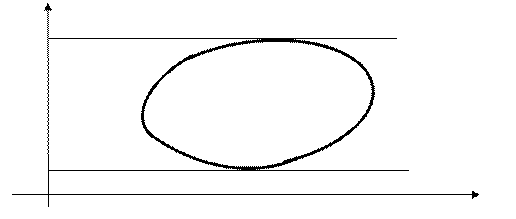у

d

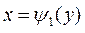
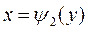
c

O x

Замечание 4. Если область неправильная, то её прямыми разбивают на несколько правильных областей. Тогда двойной интеграл по такой области равен сумме двойных интегралов по полученным правильным областям.

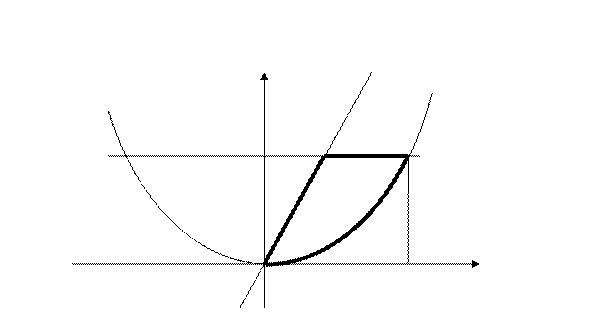Пример. Вычислить интеграл по области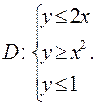

Изобразим данную область на рисунке.

у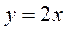

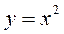
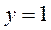
D

O 1 x

Для такой области более удобно для вычисления двойного интеграла использовать формулу (6) (почему?)

Дата добавления: 2014-11-16