Лекция № 50

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

КУРС ЛЕКЦИЙ

КНИГА — ПОЧТОЙ

САМЫЙ ПОЛНЫЙ УЧЕБНИК ДЛЯ ТРЕНЕРОВ, ПЕРЕГОВОРЩИКОВ И ВСЕХ-ВСЕХ-ВСЕХ

Елена Евгеньевна Акимова

До следующей встречи!

Главный редактор И. Авидон

Художественный редактор Л. Борозенец

Технический редактор А. Каретин

Корректор А. Борисенкова

Ответственный секретарь М. Фомичева

Генеральный директор Л. Янковский

Подписано в печать 15.09.2009 г.

Формат 70xl00 ¹/₁₆. Усл. печ. л. 18.

Тираж 2000 экз. Заказ № 1262

ООО Издательство «Речь»

199178, Санкт-Петербург, а/я 96. «Издательство „Речь"»

тел. [phone]

[e-mail]

Интернет-магазин: www.rech.spb.ru

Представительство в Москве:

тел.: [phone]

Отпечатано с готовых диапозитивов

в ГУЛ «Типография «Наука» 199034, Санкт- Петербург, 9 линия, 12

Вы можете заказать книги нашего издательства любым удобным для вас способом:

• По телефонам: [phone], [phone]

• По электронной почте: [e-mail]

• На сайте издательства: www.rech.spb.ru

• По почте: 199178, Санкт-Петербург, а/я 96,
Издательство «Речь»

Вы делаете заказ, указав:

1) фамилию, имя, отчество, телефон, e-mail;

2) почтовый индекс, регион, район, населенный пункт улицу, дом, корпус, квартиру;

3) название книги, автора, количество экземпляров.

Мы высылаем Вам книги в течение 3-х дней после принятия заказа!

по высшей математике

Часть III

Учебное пособие

Донецк - 2010

1. Основные типы уравнений математической физики

Для дифференциальных уравнений второго порядка в частных произ-водных существуют три типа уравнений или уравнений, сводящихся к ним путём замены переменных:

1. Уравнения гиперболического типа.

К этому уравнению приводятся задачи о различных колебательных процессах. Простейший (канонический) вид этого уравнения

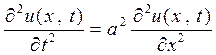- волновое уравнение.

2. Уравнения эллиптического типа.

К этому уравнению приводятся задачи об электрических и магнитных полях, задачи гидродинамики жидкости, диффузии, упругости. Каноничес-кий вид этого уравнения

- уравнение Лапласа.

3. Уравнения параболического типа.

К этому уравнению приводятся задачи о распространении тепла, фильтрации жидкости и газа. Канонический вид этого уравнения

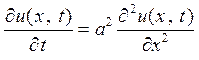- уравнение Фурье или теплопроводности стержня.

Остановимся более подробно на случае волнового уравнения.

2. Решение волнового уравнения методом Фурье

Рассмотрим задачу о колебаниях струны, закреплённой в точках и . Уравнение её поперечных колебаний имеет вид

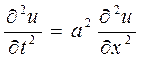, (1)

где 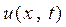- поперечное смещение струны, , T - сила натяжения струны, - линейная плотность струны.

Для решения уравнения (1) необходимо задать граничные условия (условия неподвижности концов струны):

(2)

и начальные условия (форма струны и скорость каждой точки струны в момент времени ):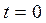

(3)

. (4)

Замечание 1. Есл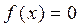и и , то струна находится в покое и .

Решение уравнения (1) будем искать в виде произведения двух функций

. (5)

Подставим выражение (5) в уравнение (1), получим

или . (6)

В левой части равенства (6) стоит функция от t, а в правой - от x. Поэтому такое равенство возможно только при условии

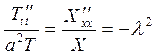или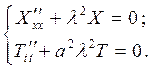

Общие решения этих дифференциальных уравнений имеют вид

,

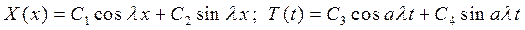тогда

(7)

Подберём произвольные постоянные , чтобы они удовлетворяли начальным и граничным условиям. Подставив выражение (7) в граничные условия (2), получим систему

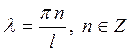Последнее равенство возможно только при , т.е. и .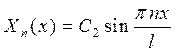

Найденные значения называются собственными значениями, а функции - собственными функциями.

Замечание 2. Константу разделения нельзя взять положительной величиной, т.е. в виде 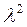, так как для этого случая решение

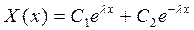
не удовлетворяет граничным условиям ни при каких значениях .

Таким образом, для каждого значения п получаем своё решение

а сумма этих решений также является решением уравнения (1), т.е.

. (8)

Теперь удовлетворим начальные условия. Подставим в условие (3) выражение (8), положив ,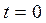

.

Замечаем, что коэффициенты являются коэффициентами Фурье разложения функции в ряд по синусам и тогда

. (9)

Продифференцируем выражение (8) по t и подставим 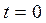, получим . (10)

Окончательно, решение уравнения (1), удовлетворяющее условиям (2-4), имеет вид (8), где коэффициенты и 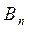вычисляются по формулам (9-10).

Пример. Решить волновое уравнение 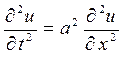при граничных условиях: и начальных условиях:

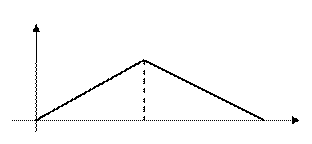
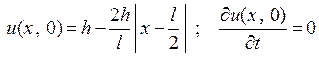. и

Так как 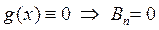, то M

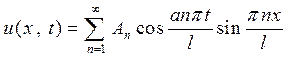, h K

где уравнения прямых ОМ и МК: О 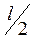l x

и тогда находим

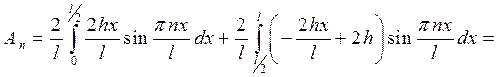
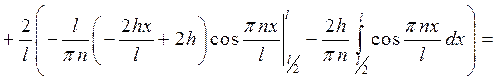
Тогда

.

Если обозначить , то

.

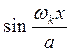Здесь - частоты колебаний, - формы колебаний с соот-ветствующими амплитудами .

Дата добавления: 2014-11-16