Лекция № 53

2.5.2. Объём тела.

Объём тела, ограниченного снизу поверхностью , сверху - , из геометрического смысла двойного интеграла вычисляется по формуле

.

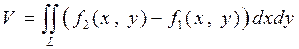Пример 1. Найти объём тела, z

ограниченного поверхностями

.

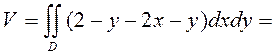
1 2 y

x

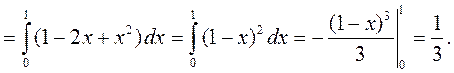
Этот результат легко проверить, если вычислить объём соответству-ющей пирамиды.

2.5.3. Площадь поверхности.

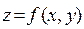Пусть поверхность с площадью задана уравнением , а её проекцией на плоскость О ху является область D.

Как известно, нормальным вектором к поверхности будет вектор 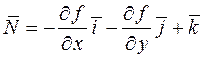. Выделим на данной поверхности элемент , проекцией которого в область D с точностью до б.м.в. более высокого порядка служит элемент .

z

y

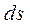
x

Так как ,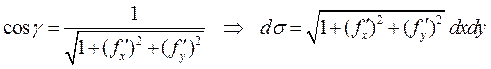

то, интегрируя , находим .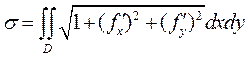

Пример 2. Найти площадь поверхности сферы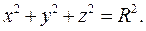

Уравнение верхней половины сферы имеет вид . Тогда

и .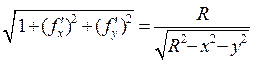

Областью интегрирования является круг .

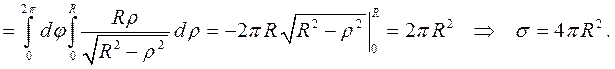
2.5.4. Масса плоской фигуры.

Как было показано ранее, масса тела, в частности плоского, с плотностью вычисляется по формуле

.

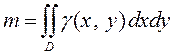Пример 3. Найти массу плоской фигуры с плотностью 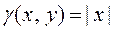, заданной областью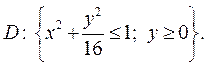

В силу симметрии имеем

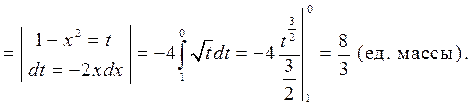
2.5.5. Центр масс (тяжести) плоского тела

Из механики известно, что координаты центра масс (тяжести) системы материальных точек определяются по формулам

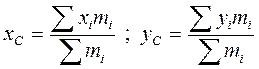. (1)

Разобьём данное плоское тело на п частей и выберем в каждой из этих частей произвольно точки 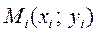. Тогда масса каждой части будет равна 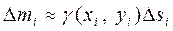, где - плотность плоского тела, и согласно формулам (1) получаем

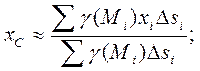
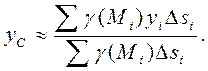
Переходя в этих формулах к пределу при 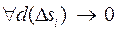, имеем

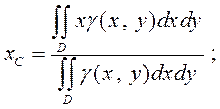
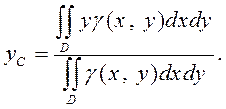(2)

Замечание. Если плоское тело однородное 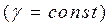, то формулы (2) принимают вид

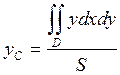; . (3)

Пример 4. Найти центр тяжести однородной равнобедренной трапеции высотой h и основаниями 2 а и 2 b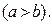

Выберем систему координат как показано на рисунке.

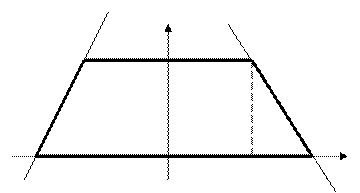Воспользуемся формулами (3) у

и проинтегрируем сначала

по х, а затем по у (почему?).

Составим уравнения сторон

трапеции, как уравнения прямых,

проходящих через две точки: - а О b a x

В силу симметрии координата . Так как площадь трапеции равна , то получим

.

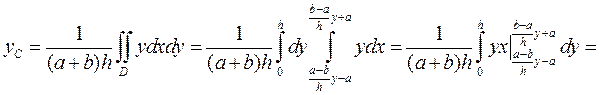
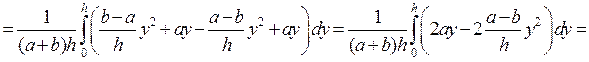
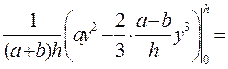
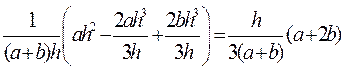2.5.6. Моменты инерции.

Аналогично можно получить формулы для нахождения моментов инерции плоской фигуры.

Для системы материальных точек моменты инерции относительно коор-динатных осей равны: ; , а относительно центра координат – .

Тогда, соответственно, если - плотность фигуры, то

Пример 5. Найти момент инерции однородного круга радиусом R относительно его центра, совпадающего с началом системы координат.

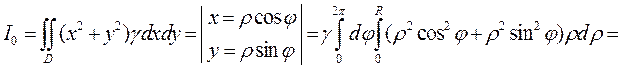
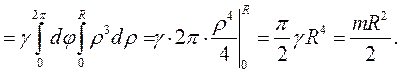
Дата добавления: 2014-11-16