
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 5 : Поверхностные интегралы
|
|
|
|
5.1. Поверхностные интегралы первого рода
Пусть в пространстве задана некоторая поверхность  , на которой определена функция
, на которой определена функция 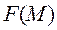 , где точка
, где точка 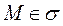 . Если в крат-ном интеграле в качестве области
. Если в крат-ном интеграле в качестве области  рассмотреть поверхность
рассмотреть поверхность  , а качестве меры – площадь этой поверхности, то получим частный случай кратного интеграла, который называется поверхностным интегралом пер-вого рода:
, а качестве меры – площадь этой поверхности, то получим частный случай кратного интеграла, который называется поверхностным интегралом пер-вого рода:
 .
.











Из определения следует, что свойства поверхностного интеграла первого рода аналогичны свойствам кратного интеграла.
Как было показано в лекции 53, элемент площади проекции поверх-ности вычисляется по формуле 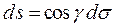 , где
, где 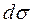 - элемент поверх-ности,
- элемент поверх-ности,
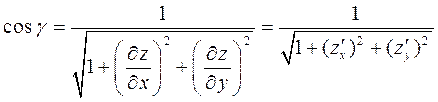
и тогда формула для вычисления интеграла принимает вид
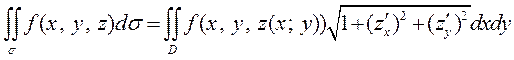 ,
,
где D - проекция поверхности  в плоскость О ху, а
в плоскость О ху, а  - уравнение поверхности
- уравнение поверхности  .
.
Замечание 2. Аналогично можно получить формулу для вычисления поверхностного интеграла первого рода в случае задания уравнений поверхности в виде  или
или  .
.
Пример 3. Вычислить  , где
, где  - часть поверхности конуса:
- часть поверхности конуса: 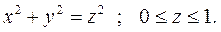
Так как уравнение поверхности в этом случае имеет вид 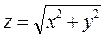 , то
, то 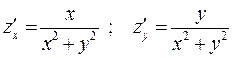 и тогда получаем
и тогда получаем
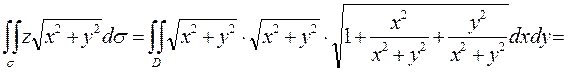
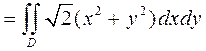 ,
,
где D - круг  .
.
Переходя к полярным координатам, получим
 .
.
5.2. Поверхностные интегралы второго рода
Пусть в каждой точке  определён некоторый вектор
определён некоторый вектор  . Разобьём поверхность на элементарные площадки
. Разобьём поверхность на элементарные площадки  и составим интегральную сумму
и составим интегральную сумму
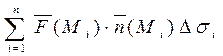 , (1)
, (1)
где  - единичный нормальный вектор поверхности.
- единичный нормальный вектор поверхности.



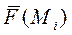













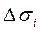
Переходя к пределу в интегральной сумме (1), получаем определение поверхностного интеграла второго рода:
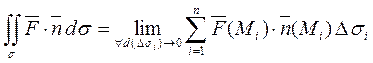 .
.
Из определения поверхностного интеграла второго рода следует:
1. Свойства интеграла аналогичны свойствам 1-2 кратных интегралов.
2. При изменении стороны поверхности интеграл меняет знак, так как меняет свое направление нормальный вектор.
Так как 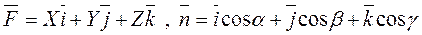
и  , то
, то
 -
-
другая запись поверхностного интеграла второго рода.
Если уравнение поверхности  , то
, то
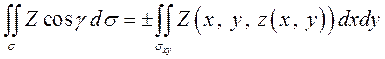 ,
,
где  - проекция
- проекция  в плоскость О ху, а знак перед интегралом берётся “+“, если
в плоскость О ху, а знак перед интегралом берётся “+“, если 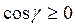 и “-“, если
и “-“, если 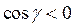 . Аналогично вычисляются инте-гралы
. Аналогично вычисляются инте-гралы 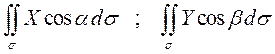 .
.
Пример 4. Вычислить  , если
, если 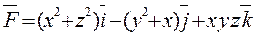 , а поверхность
, а поверхность  - грань АОС пирамиды АВСО, образованной пересече-нием плоскости
- грань АОС пирамиды АВСО, образованной пересече-нием плоскости  с координатными плоскостями.
с координатными плоскостями.
 В этом случае
В этом случае  . z
. z
 . С
. С
Тогда 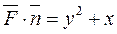 и
и 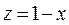


 . О В у
. О В у
А
х
5.3. Приложения поверхностных интегралов
Приложения поверхностных интегралов первого рода к задачам гео-метрии и механики аналогичны приложениям тройных интегралов, если заменить  .
.
Пример 5. Определить момент инерции однородной полусферы радиуса R относительно ее центра.
Так как
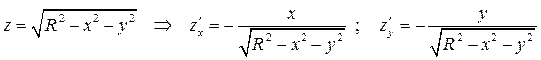 ,
,
то получим
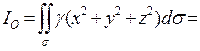

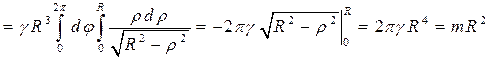 ,
,
где 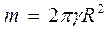 - масса полусферы.
- масса полусферы.
Если 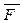 - вектор скоростей жидкости, протекающей через поверхность
- вектор скоростей жидкости, протекающей через поверхность  , то интеграл
, то интеграл

представляет собой количество жидкости, протекающей через эту поверх-ность за единицу времени (поток 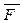 через поверхность
через поверхность  ) – физический смысл поверхностного интеграла второго рода.
) – физический смысл поверхностного интеграла второго рода.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 474; Нарушение авторских прав?; Мы поможем в написании вашей работы!