Размещения

Сочетания.

Всякое подмножество, содержащее k элементов данного множества М, состоящего из n элементов, называется сочетанием из n элементов по k.

Число сочетаний .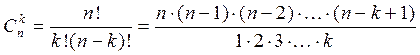

Пример 3. Сколькими способами можно выбрать трех из группы в 11 студентов?

По формуле для числа сочетаний находим количество возможных

способов выбора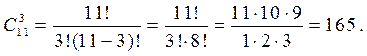

Всякое упорядоченное подмножество, содержащее k элементов данного множества М из n элементов, называется размещением из n элементов по k.

Число размещений .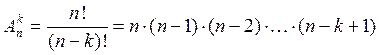

Пример 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5?

По формуле для размещений находим количество всевозможных трех-

значных чисел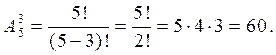

Замечание. Часто при решении задач число п достаточно велико, поэтому в таких случаях полезно использовать формулу Стирлинга

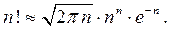
4. Основные правила комбинаторики.

Правило суммы. Если некоторый объект 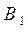можно выбрать п разными способами, а объект 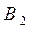можно выбрать т разными способами, причем никакой выбор 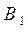не совпадает ни с каким выбором 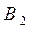, то один из объектов 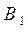или 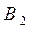можно выбрать 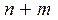способами.

Пример 5. На двух полках находится 35 и 40 книг соответственно. Сколькими способами можно выбрать одну книгу?

По правилу суммы находим число всех возможных способов выбора

Правило произведения. Если некоторый объект 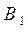можно выбрать п разными способами и при каждом выборе объекта 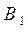объект 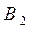можно выбрать т разными способами, то выбор пары объектов 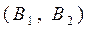можно осуществить 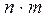способами.

Пример 6. В группе 20 студентов, из них 8 юношей и 12 девушек. Сколькими способами можно выбрать одного юношу и одну девушку для участия в конкурсе?

Каждый из п = 8 вариантов выбора юноши может комбинироваться с одним из т = 12 вариантов выбора девушки, поэтому по правилу произведения число способов выбора пары равно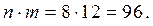

Пример 7. В группе 20 студентов, из них 8 юношей и 12 девушек. Сколькими способами можно выбрать двух юношей и трех девушек для участия в конкурсе?

Каждый из вариантов выбора двух юношей может комбинироваться с одним из 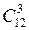вариантов выбора девушки, поэтому по правилу произведения

число способов выбора равно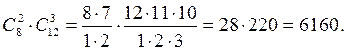

1.6. Классическое определение вероятности

Это определение относится только к тем опытам, у которых возможно конечное число равновозможных исходов. Исходы являются равновозмож-ными, если нет оснований считать, что ни один из них будет более воз-можным, чем другие. Например, если брошена игральная кость, то исходы: выпало одно очко, - два очка, …, - шесть очков – являются равно-возможными.

Определение 1. Вероятностью события А называется число 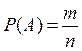, где n - число всех исходов опыта, а т - число исходов, благоприятных появлению события А.

Из определения следуют основные свойства вероятности:

1. 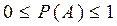, так как ;

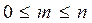2. 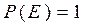, так как в этом случае ;

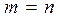3. 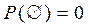, так как в этом случае .

Пример 8. Брошены две игральные кости. Найти вероятность того, что выпадет в сумме три очка.

Пусть А - интересующее нас событие. Благоприятные исходы: (1, 2) и (2, 1), т.е. . Число общих исходов определяем из того, что каждое число очков на одной кости может сочетаться с шестью вариантами числа

очков на другой кости, т.е. 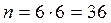. Тогда .

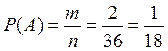Пример 9. Абонент забыл последние три цифры семизначного номера и, помня, что они различные, набрал их наугад. Найти вероятность того, что он набрал правильный номер.

Пусть А - интересующее нас событие. Очевидно, что 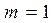. Число различных вариантов набора трёх различных цифр из десяти будет равна

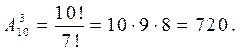Тогда .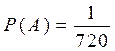

Пример 10. Некий гражданин купил карточку лото и наугад отметил 6 номеров из 49. Найти вероятность того, что он правильно угадал k номеров из 6 .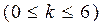

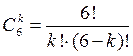Пусть А - интересующее нас событие. Общее число исходов . Число угаданных , каждый из этих вариантов может сочетаться с одним из непра-вильных вариантов.

Тогда

.

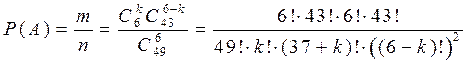Кстати, при .

1.7. Аксиоматическое определение вероятности

Аксиоматический подход основывается на основных свойствах вероятности, подмеченных на примерах классического определения и частоты.

Пусть Е - пространство элементарных событий, а 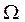- класс событий (набор подмножеств множества E). Будем считать, что в результате любых введенных выше операций над событиями, вновь получаются события этого же класса.

Пример 11. Опыт состоит из подбрасывания игральной кости один раз. Здесь 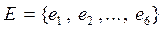. Выпишем все события, которые образуют 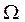. Тогда .

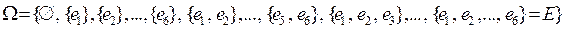Замечание. Число подмножеств множества из N элементов с учетом Е и 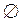равно . Например, в рассмотренном выше примере число таких подмножеств равно .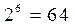

Определение 2. Числовая функция Р, определяемая на классе событий 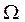, называется вероятностью, если выполнены следующие аксиомы:

1. ;

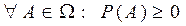2. ;

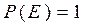3. Если несовместные события, то

.

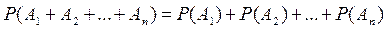Из этого определения следуют свойства:

1. .

Действительно, так как или, с учетом аксиом 2 и 3, получаем .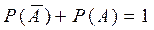

2. .

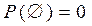Действительно, так как , то с учетом свойства 1 и аксиомы 2, получаем .

3. Если образуют полную группу событий, т.е. , то .

Это следует из аксиом 2-3.

4. .

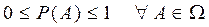Это следует из свойства 3 и аксиомы 1.

Дата добавления: 2014-11-16