Лекция № 63. Тема 5 : Числовые характеристики СВ

5.1. Математическое ожидание СВ

Часто на практике закон распределения неизвестен и приходится ограничиваться неполными сведениями о СВ. Тогда полезно использовать некоторые параметры, которые суммарно описывают СВ. Такие параметры называются числовыми характеристиками. К их числу, в частности, относится математическое ожидание.

5.1.1. Рассмотрим случай дискретной СВ.

X			…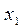
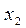
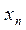
p			…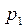

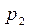
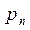
Обозначим её среднее значение через М (Х), тогда

,

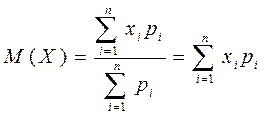так как .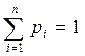

Определение 1. Математическим ожиданием дискретной СВ называ-ется величина

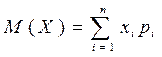. (1)

Замечание. Если число возможных значений дискретной СВ беско-нечно, то

,

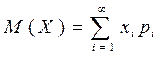при условии сходимости ряда.

Из определения математического ожидания следуют его свойства:

1. Если .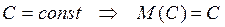

2. Если .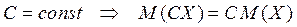

3. .

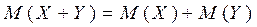Действительно, рассмотрим две СВ с законами распределения

X			…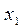
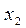
p			…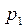

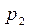
Y			…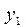
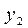
q			…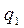

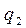
Тогда СВ 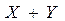- принимает возможные значения 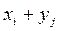с вероят-ностью 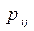и тогда

.

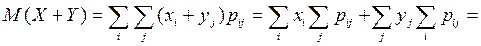
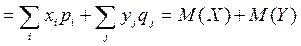4. Если Х и Y - независимые СВ, то .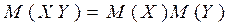

Так как 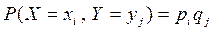, то

.

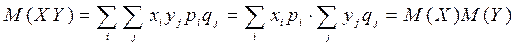Следствие. .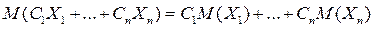

Пример 1. Найти математическое ожидание числа очков, которые могут выпасть при бросании двух игральных костей.

Пусть Х и Y - СВ выпадения очков на двух костях соответственно:

X		…
p		…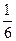

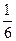
Y		…
p		…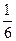

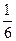
Тогда

.

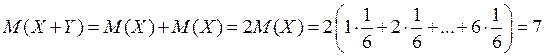5.1.2. Для непрерывной СВ выражение 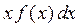представляет собой среднее значение этой СВ на интервале длиной 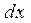и тогда её среднее значение

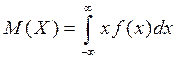. (2)

Замечание. Математическое ожидание непрерывной СВ имеет анало-гичные свойства.

5.2. Дисперсия и среднее квадратическое отклонение СВ

Математическое ожидание полностью не характеризует СВ. Поэтому вводят другие числовые характеристики.

Определение 2. Отклонением или центрированной СВ называется вели-

чина .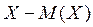

Легко показать, что .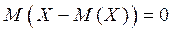

Определение 3. Дисперсией СВ называется математическое ожидание квадрата отклонения случайной величины Х от своего математического ожидания 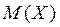и обозначается

.

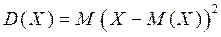Из этого определения следует, что дисперсия характеризует меру рассеивания возможных значений около её математического ожидания.

Определение 4. Величина 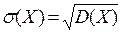называется средним квадра-тическим отклонением.

Получим более удобную формулу для вычисления дисперсии.

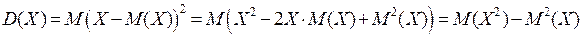. (3)

Тогда для дискретной СВ формула дисперсии примет вид

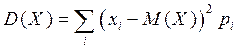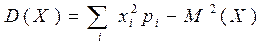или . (4)

Для непрерывной СВ -

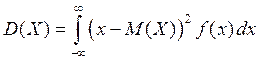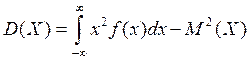или . (5)

Свойства дисперсии:

1. 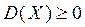, как сумма неотрицательных членов, или как интеграл от неотрицательной функции.

2. 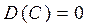, так как .

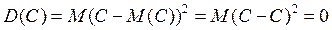3. 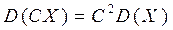, что следует непосредственно из определения дисперсии.

4. Если Х и Y независимые СВ, то .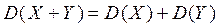

Действительно,

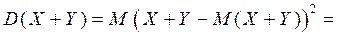
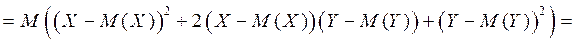
(и с учетом свойств математического ожидания)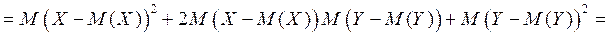

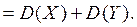
Пример 2. Найти математическое ожидание 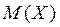, дисперсию 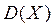и среднеквадратическое отклонение 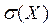случайной величины с плот-ностью распределения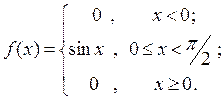

По формулам (2), (4-5) соответственно находим:

.

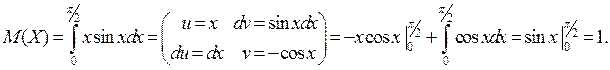
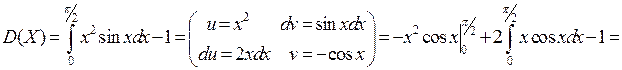
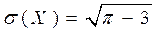5.3. Понятие о моментах СВ

Кроме математического ожидания 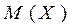и дисперсии 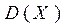ис-пользуются и другие числовые характеристики СВ.

Определение 5. Начальным моментом k -го порядка СВ называется величина .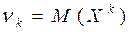

Тогда для дискретных СВ: .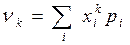

Для непрерывных СВ: .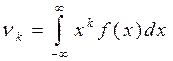

Определение 6. Центральным моментом k -го порядка СВ называется величина .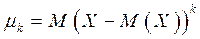

Тогда для дискретных СВ: .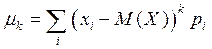

Для непрерывных СВ: .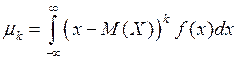

Легко проверить следующие соотношения:

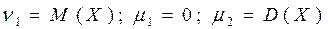
и установить связь между начальными и центральными моментами:

.

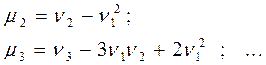Моменты характеризуют то или иное свойство СВ. Например, 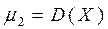(дисперсия) характеризует рассеивание значений СВ около математического ожидания 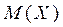, 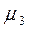- асимметрию распределения и т.д.

Дата добавления: 2014-11-16