Лекция № 66. Тема 8 : Многомерные случайные величины

8.1. Многомерные СВ и их функции распределения

Определение 1. Многомерной случайной величиной называется вектор, координаты которого являются СВ, т.е. .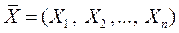

Например, координаты точки попадания при выстреле – двумерная СВ; станок изготовляет детали длиною X, внутренним диаметром Y, внешним диаметром Z - трёхмерная СВ (X, Y, Z).

Ограничимся случаем двумерной СВ (X, Y). Законом распределения дискретной двумерной СВ является перечень её возможных значений и соответствующих им вероятностей. Его удобно задавать в виде таблицы.

Y X			…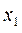
			…
			…
…	…	…	…	…
			…

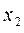
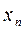
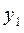
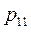
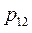
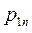
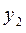
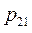
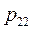
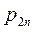
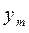
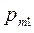
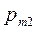
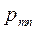
Здесь .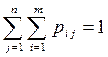

Аналогично, как и в случае одномерной СВ, обозначим через 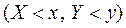- множество элементарных событий, для которых одно-временно выполняются неравенства 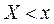и .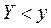

Определение 2. Функцией распределения двумерной СВ называется 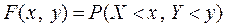. у

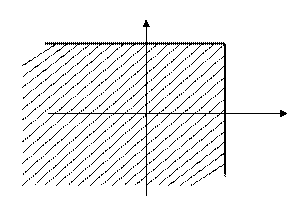
Геометрически функция 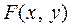(х, у)

представляет собой вероятность

попадания случайной величины

(X, Y) в бесконечный квадрат х

с вершиной в точке (х, у).

Из определения функции

распределения следуют ее свойства.

1.

2. 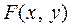- неубывающая функция.

3.

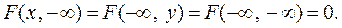
4. 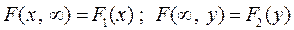, где и 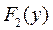- функции распределения СВ X и Y соответственно.

5.

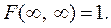
Рассмотрим предел .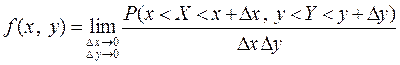

Можно показать, что этот предел равен 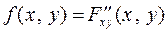- плот-ности распределения двумерной СВ.

Свойства плотности распределения:

1. 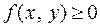, так как 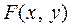неубывающая функция.

2. Вероятность попадания СВ (X, Y) в область D равна

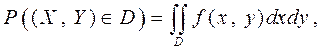
так как 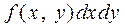- вероятность попадания в прямоугольник пло-щадью .

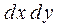3. 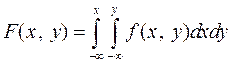, что следует из определения .

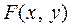4. 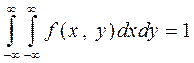, что следует из свойства 3 и того, что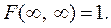

5.

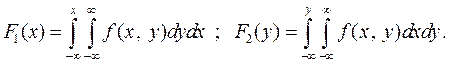
Определение 3. СВ X и Y называются независимыми, если 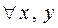выполняется равенство

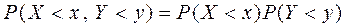
или

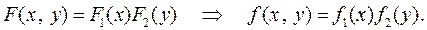
Пример 1. Определить зависимы или независимы СВ X, Y и найти вероятность их попадания в квадрат 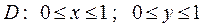, если

.

Имеем 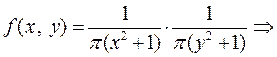X и Y - независимые СВ.

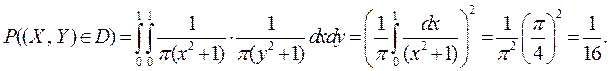
8.2. Числовые характеристики двумерной случайной величины

Числовые характеристики составляющих двумерной СВ вводятся также как и для одномерной. Кроме таких числовых параметров вводятся и такие, которые характеризуют зависимость составляющих X и Y.

Определение 4. Ковариацией двумерной СВ называется

.

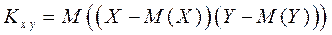После простых преобразований можно получить

.

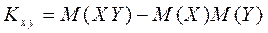Очевидно, 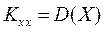. Для дисперсии суммы ранее была получена формула (лекция 63)

.

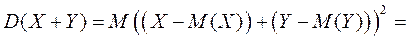
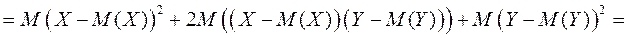
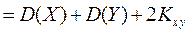Тогда для независимых СВ 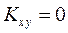. Таким образом, если 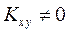, то случайные величины X и Y зависимы.

Для характеристики степени зависимости случайных величин X и Y используется коэффициент корреляции

.

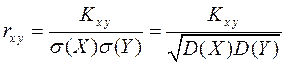Отметим его основные свойства.

1. Если СВ X и Y независимы, то коэффициент корреляции 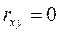. Обратное, вообще говоря, неверно.

2. Если 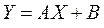, где А и В , то .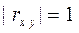

Действительно, обозначим 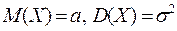, тогда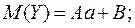

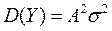и

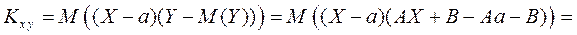
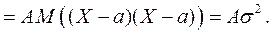
После этого получаем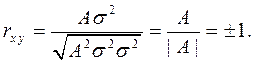

3. .

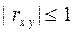Замечание. Из определения и свойств коэффициента корреляции сле-дует, что он оценивает линейную связь между X и Y. При этом:

1. 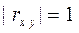- функциональная линейная связь.

2. - статистическая зависимость.

3. 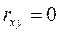- линейная связь отсутствует.

Пример 2. Закон распределения СВ (X, Y) задан таблицей

Y X
	0,17	0,13	0,25
	0,1	0,3	0,05

Найти законы распределения составляющих и числовые характеристики.

Проводя суммирование по соответствующим строкам и столбцам, получаем

Y				Х
p	0,55	0,45		p	0,27	0,43	0,3

Вычислим числовые характеристики:

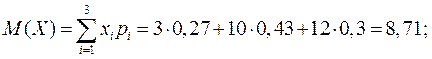
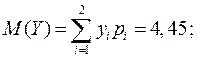
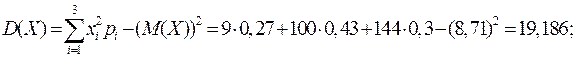
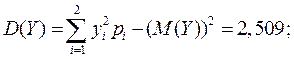
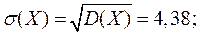
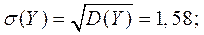
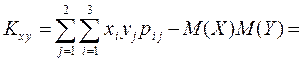
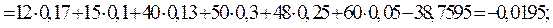
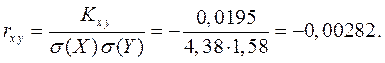
Найденный коэффициент корреляции мал, следовательно, СВ X и Y слабо зависимы.

Дата добавления: 2014-11-16