Тема 4 : Элементы теории корреляции

.....

[ [ [ [ [

Здесь 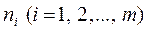- частота появления признака, принадлежащего интервалу . Очевидно, что объём выборки .

Теоретические частоты , соответствующие эмпирическим, вычис-лены по предполагаемому закону распределения (гипотеза), для них также выполняется равенство

Величина 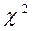является случайной величиной, при этом ее распреде-ление не зависит от функции распределения случайной величины X и стре-мится при 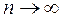к так называемому 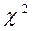-распределению с 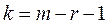степенями свободы, где r - число параметров теоретического закона.

Из этого следует критерий для проверки гипотезы о распределении изучаемой случайной величины (критерий Пирсона). Рассмотрим его при-менение для проверки гипотезы о нормальном распределении.

Пусть эмпирическое распределение задано в виде вариационного ряда равноотстоящих вариант с шагом h

			…
			…

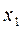
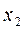
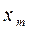
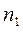
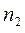
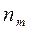
Необходимо:

1. Вычислить выборочное среднее

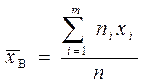
и исправленное выборочное среднее квадратическое отклонение

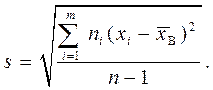
2. Определить теоретические частоты, считая закон распределения нормальным, т.е.

, (2)

где

.

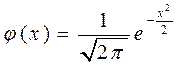3. По формуле (1) вычислить величину 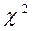. Пусть она оказалась равной .

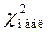4. Определить число степеней свободы для нормального распределения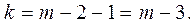

5. По таблице критических точек распределения 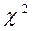, по заданному уровню значимости 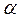и числу степеней свободы k находим критическую точку 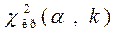. Если 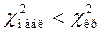, то гипотеза о нормальном распределении принимается, т.е. эмпирические и теоретические частоты различаются незначительно. В противном случае гипотеза отвергается.

Уровень значимости 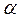означает, что вероятность 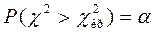, т.е. осуществление такого события практически невозможно.

Замечание 1. Рассмотренный критерий на практике даёт хорошие результаты, если .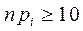

Пример 1. Проверить, согласуются ли данные таблицы с предполо-жением, что рост мужчины является нормально распределённой случайной величиной, приняв уровень значимости

			0,0370
			0,1420
			0,0201
			0,1429
			0,0328
			0,0606
			0,8182
Итого			1,2536

Из таблицы следует, что 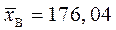, 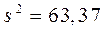и теоретические частоты определяем по формуле (2).

Таким образом, 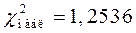. По уровню значимости и числу степеней свободы 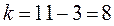по таблице критических точек распределения 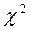находим 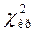= 20,1. Так как 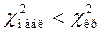, то гипотеза принимается.

4.1. Статистические зависимости

Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от другой случайной величины Х.

Две случайные величины могут быть связаны определённой зависимостью, которую принято называть статистической, или быть независимыми.

Определение 1. Статистической называется зависимость, при которой изменение одной случайной величины Х влияет на распределение другой случайной величины Y. Если при этом изменяется еще и среднее значение случайной величины Y, то такая зависимость называется корреляционной.

Например, пусть Х - сумма затрат на подготовку лавы, а Y - уровень добычи угля. При одинаковых затратах на подготовку лав добыча угля будет отличаться, т.е. СВ Y не является функцией от Х. Это можно объяснить влиянием случайных факторов (глубиной залегания пласта, его мощностью, сортностью угля и т.п.). Тем не менее, средняя добыча угля является функцией от суммы затрат, т.е. случайные величины Y и Х связаны корреляционной зависимостью.

4.2. Линейная регрессия

Определение 2. Выборочным уравнением линейной регрессии случайной величины Y на Х называется уравнение вида

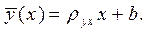(3)

Уравнение (3) часто называют просто уравнением линейной регрессии, а угловой коэффициент - выборочным коэффициентом регрессии.

Для отыскания выборочного уравнения регрессии воспользуемся методом наименьших квадратов, т.е. мы должны минимизировать функцию суммы квадратов отклонений

Как было показано ранее, в этом случае коэффициенты уравнения (3) определяются по формулам

(4)

где

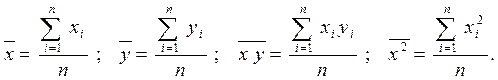
Пример 2. Найти выборочное уравнение линейной регрессии СВ Y на Х по данным 10 наблюдений:

п
X	1,5	2,5	3,0	3,5	5,0	6,0	7,5	8,5	9,0	9,5
Y	11,0	10,0	9,0	8,0	7,5	7,5	7,0	6,5	5,5	5,0

Составим расчетную таблицу:

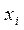
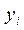
1,5	11,0	2,25	16,50
2,5	10,0	6,25	25,00
3,0	9,0	9,00	27,00
3,5	8,0	12,25	28,00
5,0	7,5	25,00	37,50
6,0	7,5	36,00	45,00
7,5	7,0	56,25	52,50
8,5	6,5	72,25	55,25
9,0	5,5	81,00	49,50
9,5	5,0	90,25	47,50

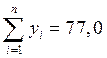
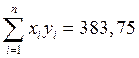
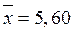
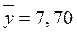
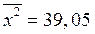
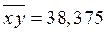
По формулам (4) получим и .

Таким образом, линейная регрессия имеет вид .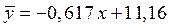

Проверим, насколько хорошо полученные результаты согласуются с наблюдаемыми данными. Найдем отклонения

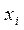
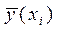
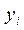
1,5	10,23	11,0	-0,77
2,5	9,62	10,0	-0,38
3,0	9,31	9,0	0,31
3,5	9,00	8,0	1,00
5,0	8,08	7,5	0,57
6,0	7,46	7,5	-0,04
7,5	6,53	7,0	-0,47
8,5	5,92	6,5	-0,58
9,0	5,61	5,5	0,11
9,5	5,30	5,0	0,30

Как видим из таблицы, не все отклонения достаточно малы. Это объясняется недостаточным количеством наблюдаемых данных.

4.3. Корреляционная таблица

При большом числе наблюдений одно и то же значение СВ Х может встретиться раз, одно и то же значение СВ Y может встретиться раз, а одна и та же пара чисел (х, у) может наблюдаться раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты , , . Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Поясним ее строение на простом примере. Имеем таблицу:

Y X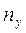
-1

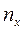
В первой строке указаны наблюдаемые значения (1, 2, 3, 4, 5) случайной величины Х, а в первом столбце – наблюдаемые значения (-1, 0, 1, 2) случайной величины Y. На пересечении строк и столбцов находятся частоты наблюдаемых пар значений СВ Х и Y. Например, частота 6 указывает, что пара чисел (4, -1) наблюдалась 6 раз. Все частоты помещены в прямоугольнике, стороны которого проведены жирными линиями.

В последнем столбце записаны суммы частот строк. Например, сумма частот второй строки равна 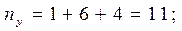это число указывает, что значение случайной величины Y, равное 0 (в сочетании с различными значениями СВ Х), наблюдалось 11 раз.

В последней строке записаны суммы частот столбцов. Например, сумма частот четвертого столбца равна 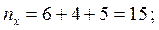это число указывает, что значение случайной величины Х, равное 4 (в сочетании с различными значениями СВ Y), наблюдалось 15 раз.

Общее число наблюдений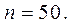

4.4. Выборочный коэффициент корреляции

Ранее мы полагали, что значения Х и соответствующие им значения Y наблюдались по одному разу. На практике, безусловно, одна пара случайных величин (х, у) может наблюдаться любое число раз.

Поэтому формула для коэффициента регрессии (4) примет вид

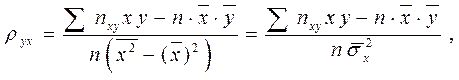(5)

где в сумме 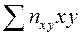учтено, что пара (х, у) наблюдалась 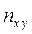раз, а и - выборочные средние квадратические отклонения.

Умножим обе части равенства (5) на дробь и назовем это выражение выборочным коэффициентом корреляции

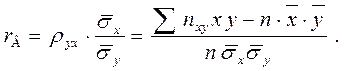
Тогда уравнение линейной регрессии Y на Х будет иметь вид

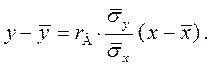
Замечание 2. Выборочный коэффициент корреляции является безраз-мерной оценкой коэффициента регрессии

Таким образом, основная задача корреляционного анализа состоит в оценке степени линейной связи между случайными величинами Х и Y, кото-рая устанавливается при помощи выборочного коэффициента корреляци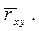и Если мал, то линейная связь считается слабой и ее можно не при-нимать во внимание. Если же коэффициент корреляции близок к 1, то линейная связь сильная и к ней следует относиться практически как к функ-циональной. В противном случае, связь считается статистической. И, нако-нец, при 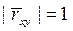связь между случайными величинами Х и Y имеет строго линейный характер.

Дата добавления: 2014-11-16