Тема 2 : Статистические оценки параметров распределения

2.1. Точечные оценки

Приближенные значения числовых параметров распределения называ-ются оценками. Различают точечные и интервальные оценки. Первые дают приближенные числовые значения изучаемого параметра 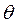, вторые – устанавливают вероятность покрытия этого параметра некоторым интер-валом, называемого доверительным.

К точечным оценкам параметров распределения случайной величины предъявляют следующие требования:

1. Состоятельности: Если 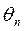точечная оценка параметра 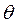, то ;

2. Несмещенности: , т.е. математическое ожидание оценки 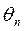равно оцениваемому параметру;

3. Эффективности: , т.е. дисперсия принимает минималь-ное значение.

Точечной оценкой для математического ожидания служит выборочное математическое ожидание:

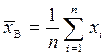, если все варианты различны,

а в противном случае - .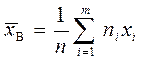

Эта оценка удовлетворяет всем трём требованиям.

Точечной оценкой для дисперсии служит выборочная дисперсия

или .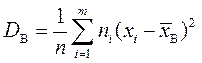

Эта оценка является состоятельной и эффективной, но для нее, как можно показать, выполняется

,

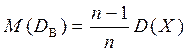т.е. данная оценка является смещенной.

Это можно устранить, если ввести исправленную дисперсию 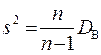, которая будет удовлетворять всем трём требованиям.

2.2. Интервальные оценки

Пусть для некоторого числового параметра 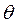из опыта получена несмещённая оценка 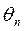. Оценим возможную при этом ошибку. Зададим некоторую вероятность 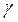(доверительная вероятность или надёжность) и найдём такое число (точность оценки), для которого выполняется

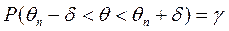или . (1)

Равенство (1) нужно понимать так: вероятность того, что интервал (доверительный интервал) покрывает параметр 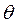равна .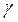

Ограничимся нахождением доверительного интервала для математи-ческого ожидания нормального распределения для двух случаев:

1. Известно среднее квадратическое отклонение 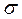, тогда

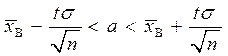или , (2)

где параметр t определяется по таблицам из условия

или .

Из оценки (2) можно сделать два вывода:

а) при возрастании объема выборки п величина убывает, следо-вательно, точность оценки увеличивается;

б) из увеличения надежности оценки следует увеличение параметра t и, соответственно, величины , следовательно, увеличение надежности уменьшает точность оценки.

Пример 4. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 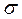= 5. Найти доверитель-ный интервал для оценки неизвестного математического ожидания а по выборочным средним , если объем выборки п = 100 при заданной надежности

Из соотношения 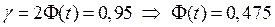по таблице находим параметр t = 1,96. Тогда точность оценки

Таким образом, доверительный интервал 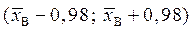или

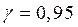Например, если найденное выборочное среднее , то с веро-ятностью математическое ожидание случайной величины Х попадает в доверительный интервал .

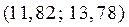2. Среднее квадратическое отклонение 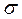неизвестно. Тогда

,

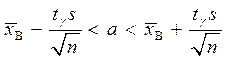где s - исправленное среднее квадратическое отклонение, а 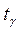находится по таблицам критических значений так называемого распределения Стьюдента по значениям 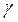и n.

Пример 5. После проверки размера (в мм) выбранных 100 однотипных изделий получен вариационный ряд

	15,7	15,8	15,9	16,0	16,1	16,2

Найти доверительный интервал для оценки неизвестного математичес-кого ожидания а при заданной надежности считая распреде-ление нормальным.

Найдем выборочное среднее и дисперсию

По таблице с учетом объема выборки п = 100 и заданной надеж-ности находим параметр t = 2,627. Тогда точность оценки

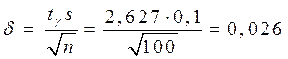
и доверительный интервал 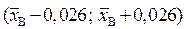или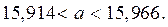

Дата добавления: 2014-11-16