Тема 7 : Закон больших чисел

Этот закон обосновывает устойчивость средних, т.е. при очень большом числе случайных событий их средний результат практически перестаёт быть случайным и может быть предсказан с большой точностью. Какие условия необходимы для этого?

7.1. Неравенство Чебышева

Теорема 1. Если случайная величина Х имеет конечную дисперсию, то для справедливо неравенство

.

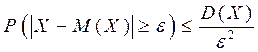Доказательство проведём для непрерывной СВ.

Из рисунка

х

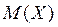
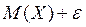
следует

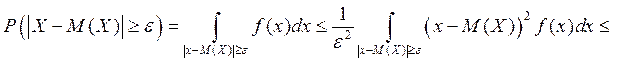
что и требовалось доказать.

Пример 3. Дана случайная величина Х с математическим ожиданием и дисперсией . Оценить вероятность того, что случайная величина Х отклонится от своего математического ожидания не менее, чем на .

Положим в неравенстве Чебышева , тогда верхняя граница вероятностей

,

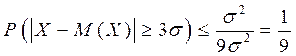что верно для всех законов распределения СВ.

7.2. Теорема Чебышева

Теорема 2. Если 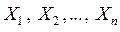- независимые СВ, имеющие конечные дисперсии, т.е. 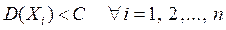, то

Рассмотрим новую СВ 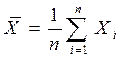и применим к ней неравенство Чебышева

.

Переходя к пределу при 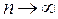и, учитывая что 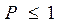, получаем теорему Чебышева.

Следствия:

1. Теорема Бернулли. Если - число наступления события А в п независимых испытаниях, а р - вероятность А, то

Пусть - число появления события A в одном испытании, т.е.

p	q	p

Тогда 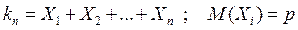и

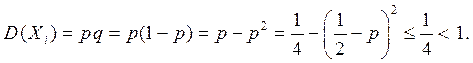
Подставляя в неравенство Чебышева соответствующие значения, полу-чаем теорему Бернулли.

2. Если для последовательности независимых случайных величин вы-полняется равенств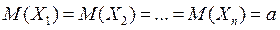о , то

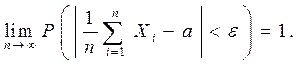
Доказательство следует из теоремы Чебышева.

Этот частный случай даёт основание правилу среднего арифметичес-кого, употребляемого в теории измерений, т.е. если результаты измерений: 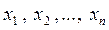, то искомая величина . Следовательно, увеличивая число измерений, мы получим более надежный результат.

Пример 3. Дисперсия каждой из попарно независимых случайных величин не превышает 10. Оценить вероятность того, что отклонение среднего арифметического 16000 этих величин от среднего арифметического их математических ожиданий не превосходит 0,25.

По условию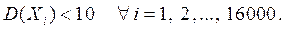

Тогда по теореме Чебышева С = 10 и искомая вероятность

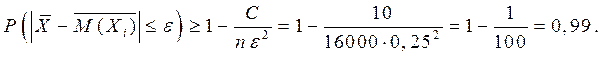
Дата добавления: 2014-11-16