Лекция № 65

6.2.3. Нормальное распределение

Определение 3. СВ X называется распределённой по нормальному закону, если функция плотности распределения .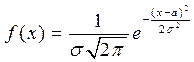

Определим смысл параметров a и 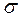. Для этого вычислим:

,

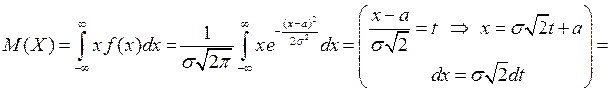
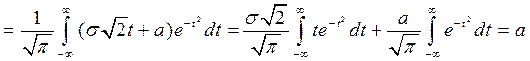так как первый интеграл равен нулю, как интеграл от нечетной функции в симметричных пределах, а второй является интегралом Пуассона.

Таким образом, . Аналогично можно показать, что 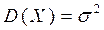, т.е. .

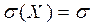График функции нормального распределения имеет вид (Лекция 22)

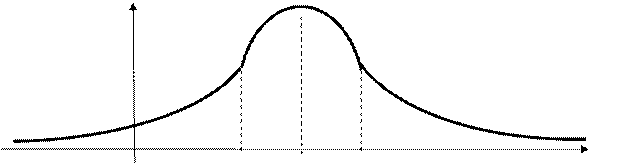
f (х)

О а х

Здесь 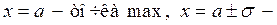точки перегиба, .

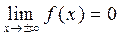Если вычислить значения центральных моментов

,

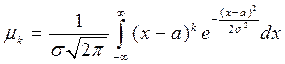то получим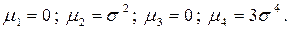

Часто на практике в качестве числовых характеристик используются так называемые эксцесс - Ex и коэффициент асимметрии - As. В частности, для нормального распределения они равны:

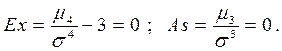
Таким образом, эти коэффициенты определяют степень отклонения распределений от нормального.

Вероятность попадания в заданный интервал случайной величины, имеющей нормальное распределение, определяется по формуле

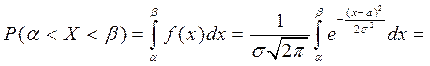
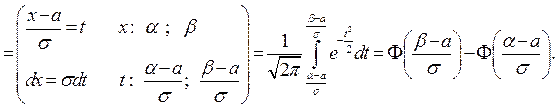(1)

Следствие 1. Пр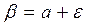и и 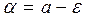из формулы (1) получаем

. (2)

Следствие 2. Если положить в формуле (2) 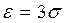и учесть, что при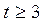 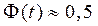, то получим

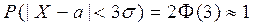. (3)

Выражение (3) представляет собой так называемое правило трёх сигм. Оно означает, что практически в интервале 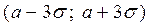находятся все возможные значения нормально распределённой СВ.

Нормальный закон распределения играет в теории вероятностей важную роль, так как является предельным законом, к которому приближаются многие другие законы. Это отражено в центральной предельной теореме Ляпунова.

Теорема. Если Х - сумма большого числа независимых случайных величин 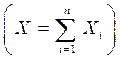, которые имеют различные распределения и их влияние на СВ Х незначительно, то Х имеет распределение близкое к нормальному. А в пределе СВ Х стремится к нормальному закону.

Нормальный закон широко используется в теории ошибок, в теории стрельбы, теории надёжности и т.д.

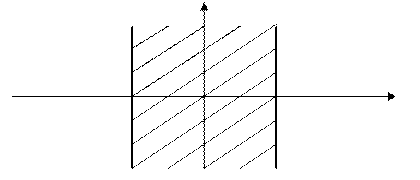
Пример 3. По цели, имеющей вид полосы, ширина которой 20 м, ведётся стрельба в направлении перпендикулярном полосе. Прицеливание ведётся по средней линии. Среднее квадратическое отклонение (точность прицела) в направлении стрельбы равна 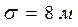. Найти вероятность попадания в цель при одном выстреле.

у

-10 а = 0 10 х

Здесь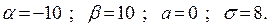

Подставляя в формулу (2) эти значения, получим

Дата добавления: 2014-11-16