Лекция № 61. Тема 3 : Повторение испытаний

3.1. Независимые испытания. Формула Бернулли

Испытание – это осуществление определённых условий, в результате которых может произойти то или иное элементарное событие простран-ства E. Если число исходов испытания - m, то назовём событие - i -м исходом . Обозначим и будем считать, что все

события образуют полную группу событий, тогда

Пусть произведено n испытаний.

Определение 1. Если исходы испытания в каждом опыте не зависят от предыдущих исходов, то такие испытания называются независимыми.

Например, при бросании игральной кости, исходы: выпало одно, два очка и т.д. не зависят от предыдущих очков – испытания независимые.

Рассмотрим случай (схема Бернулли). Положим , т.е. .

Рассмотрим следующую задачу. Пусть произведено n независимых испытаний, в каждом из которых событие A может появиться с одной и той же вероятностью р. Требуется найти - вероятность того, что событие А появится k раз, а событие появится раз.

Рассмотрим в какой либо последовательности чередование событий А и так, чтобы А повторялось k раз, а событие появилось раз. Это событие . По теореме умножения вероятностей получаем

.

По теореме сложения вероятностей равна сумме таких вероятностей для всех различных способов появлений события А (k раз из п), т.е. их число . Поскольку все эти вероятности равны, то получаем формулу Бернулли

. (1)

Замечание 1. Так как все возможные исходы: событие А появилось 0 раз, 1 раз, …, п раз образуют полную группу событий, то

Пример 1. Вероятность хотя бы одного попадания при двух выстрелах равна 0, 96. Найти вероятность трёх попаданий при четырёх выстрелах.

Если - вероятность хотя бы одного попадания при двух выст-релах, то

,

тогда вероятность одного попадания и вероятность трёх попаданий при четырёх выстрелах

3.2. Локальная теорема Муавра – Лапласа

При больших значениях n формулу (1) использовать затруднительно. Поэтому возникает вопрос о замене её некоторой асимптотической формулой, т.е. приближенной, справедливой при больших п.

Теорема 1. Если вероятность появления события А в каждом из независимых испытаний постоянна и равна р, то вероятность при больших п приближенно равна значению функции

, где при . (2)

Значения функции берутся из таблиц, при этом - четная функция, т.е. .

Пример 2. Вероятность рождения мальчика равна 0,51. Найти вероят-ность того, что среди 100 новорожденных окажется половина мальчиков.

Вероятность такого события вычисляем по формуле (2) при и . Имеем

где значение взято из таблицы значений функции .

3.3. Интегральная теорема Лапласа

Пусть производится п независимых испытаний. Как найти вероятность того, что событие А появится в п испытаниях не менее раз и не более раз? Формулой пользоваться не удобно. Ответ даёт теорема

Теорема 2. Если вероятность появления события А в каждом из п независимых испытаний постоянна и равна р, то вероятность при больших п приближенно равна

,

где

(3)

Для приближенного вычисления данного интеграла

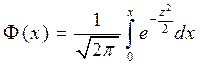(функция Лапласа)

имеются таблицы, при этом 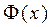функция нечетная, т.е. .

Тогда

.

Замечание 2. Погрешность вычислений вероятностей по формулам (2) и (3) имеет порядок .

Пример 3. Вероятность того, что деталь прошла проверку ОТК, равна 0,2. Найти вероятность того, среди 400 отобранных наудачу деталей окажется непроверенных от 70 до 100.

Вычислим

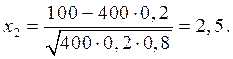
Тогда

3.4. Теорема Пуассона

Из замечания 2 следует, что точность вычисления вероятностей тем хуже, чем меньше р или q. Возникает задача отыскания асимптотической формулы, специально приспособленной для этого случая. Такая формула была получена Пуассоном.

Теорема 3. Если число испытаний велико, а вероятность появления события А в каждом испытании мала, то имеет место приближенная формула

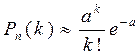или , (4)

где - среднее число появлений события А в п испытаниях.

Замечание 3. Можно проверить, что при больших п справедливо равенство

Пример 4. Вероятность того, что деталь окажется бракованной, равна 0,01. Найти вероятность того, среди 400 изготовленных деталей окажется пять бракованных.

Так как число испытаний велико, а вероятность мала, то воспользуемся формулой (4). Найдём и тогда

Замечание 4. Для удобного использования формулы Пуассона также существуют таблицы для . Есть таблицы и для вычисления вероятностей вида

(5)

причем поскольку в формуле Пуассона число испытаний достаточно велико, то п можно не писать, т.е. и

Пример 5. Вероятность того, что деталь будет забракована, равна 0,01. Найти вероятность того, что среди 400 изготовленных деталей буде не больше пяти забракованных.

Очевидно, что поэтому можем воспользо-ваться формулою (5). Из таблицы, учитывая, что и 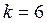, нахо-дим Следовательно, искомая вероятность равна

3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях

Пусть производится п независимых испытаний с постоянной вероят-ностью р. Требуется найти вероятность того, что отклонение частоты от р по абсолютной величине не превосходит данного , т.е.

Преобразуем неравенство в скобках

и умножим полученное неравенство на

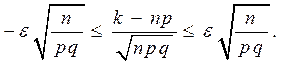
Полагая в формуле (3) и учитывая нечетность функции Лапласа, получаем

. (5)

Пример 6. Вероятность появления события А в каждом из независимых испытаний равна 0,2. Найти число испытаний п, при котором с вероят-ностью 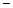0,9876 можно ожидать, что

Подставим данные задачи в формулу (5)

По таблице значений функции Лапласа 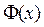находим соответствующее значение аргумента

Дата добавления: 2014-11-16