Лекция № 60. Тема 2 : Основные теоремы теории вероятностей

2.1. Теорема умножения вероятностей

Определение 1. Условной вероятностью события B при условии, что событие A произошло, называется вероятность, определяемая формулой

. (1)

Это можно легко показать для случая классического определения веро-ятности. Будем считать, что формула справедлива в общем случае и про-иллюстрируем её на примере.

Пример 1. В урне 3 белых и 3 синих шара. Из урны вынут один шар, затем второй. Рассмотрим два события: A – первым вынут белый шар, В – вторым вынут синий, тогда АВ – вынуты по очереди белый и синий шары. Найдем вероятности: . Подста-вив эти вероятности в формулу (1), убеждаемся, что она справедлива.

Определение 2. Есл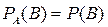и и 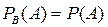, то такие события называются независимыми.

Теорема 1. . (2)

Это следует из формулы (1).

Следствие 1. Для независимых событий .

Следствие 2. Если обозначить и 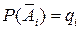, то вероятность появления хотя бы одного из событий, независимых в совокупности, равна

. (3)

Рассмотрим событие - ни одного не наступило. Тогда по следствию 1 из определения вероятности получаем

.

2.2. Теорема сложения вероятностей

Теорема 2. 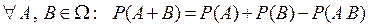. (4)

Из диаграммы событий легко получить равенства:

,

где и 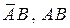- попарно

несовместные события. А В

Тогда, согласно третьей аксиоме,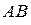

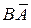
получаем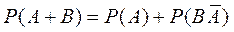

и .

Если из последнего равенства выразить и подставить в первое, то получим формулу (4).

Следствие 3. Если А и В - несовместные события, то получаем третью аксиому.

Пример 2. Вероятности попадания при двух выстрелах соответственно равны . Найти вероятность поражения цели.

Вероятность поражения цели представляет собой событие 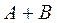, где событие А - поражение цели при первом выстреле, а событие В - поражение при втором выстреле.

Первый способ: По теореме сложения вероятностей получаем

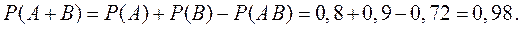
Второй способ: По формуле (3) получаем

.

Пример 3. Устройство содержит три независимо работающих элемента. Вероятности отказа элементов соответственно равны: 0,05; 0,06; 0,08. Найти вероятности событий:

1. Откажет один элемент.

Введём события: А - интересующее нас событие; В - отказал первый элемент; С - отказал второй элемент; D - отказал третий элемент.

Тогда

и, согласно теоремам об умножении и сложении вероятностей, получим

2. Ни один элемент не откажет.

Здесь интересующее нас событие 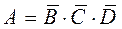и тогда

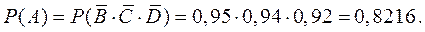
2.3. Формула полной вероятности

Пусть событие А может наступить при условии появления одного из событий , образующих полную группу событий. Будем называть их гипотезами. Пусть известны вероятности гипотез: 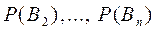и условные вероятности: 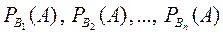. Тогда имеет место формула полной вероятности

Теорема 3.

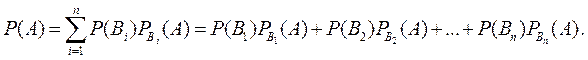(5)

Представим событие А в виде

.

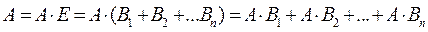Так как события 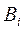попарно несовместны, т.е. 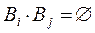, то и .

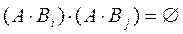Тогда по третьей аксиоме и теореме умножения вероятностей получим

.

Пример 4. Три станка выпускают одинаковую продукцию. Первый станок выпускает 20%, из них – 5% брака, второй - 30% и 3% брака, третий - 50% и 2% брака. Из общей партии берётся наудачу деталь. Какая вероятность того, что эта деталь бракована?

Пусть А - интересующее нас событие, в качестве гипотез рассмотрим события:

- деталь изготовлена на первом станке,

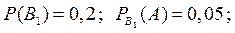
- деталь изготовлена на втором станке,

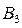- деталь изготовлена на третьем станке,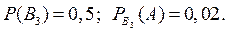

Тогда по формуле (5) получим

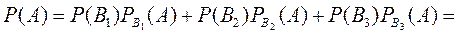
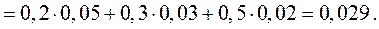
2.4. Формула Бейеса

Условия такие же, как и для формулы полной вероятности. Пусть событие А произошло, тогда вероятности гипотез могут быть переоценены по формуле Бейеса.

Теорема 4. 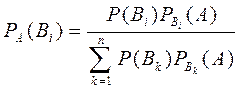. (6)

По теореме умножения вероятностей имеем

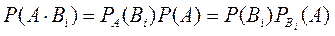
или, с учетом формулы полной вероятности, получаем

.

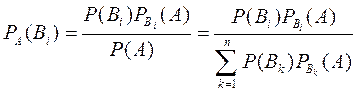Пример 5. Число грузовых автомашин, проезжающих по шоссе, на котором находится бензоколонка, относится к числу легковых как 3:2. вероятность того, что будет заправляться грузовая равна 0,1, легковая – 0,2. К заправке подъехала машина. Найти вероятность того, что она грузовая.

Введём гипотезы:

- подъехала грузовая машина,

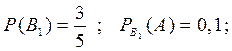
- подъехала легковая машина,

Тогда по формуле (6) получаем

Дата добавления: 2014-11-16