Лекция № 57. Тема 6 : Элементы теории поля

6.1. Понятие поля

Определение 1. Полем называется область пространства, в каждой точке которой определено рассматриваемое значение физической характеристики среды.

Эти характеристики могут быть скалярными (например, температура, давление, плотность и т.д.) или векторными (скорость, сила и т.д.).

Соответственно и поля называются скалярными и векторными.

Для задания скалярного поля достаточно задать одну функцию . Для задания векторного поля 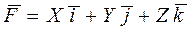необходимо задать три скалярные функции:

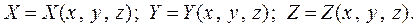
Геометрические образы поля позволяют наглядно представить его структуру. Геометрическими образами скалярного поля являются поверхности уровня (в трёхмерном пространстве) или линии уровня (в двумерном пространстве). Они соответственно задаются уравнениями: ,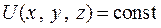

Для векторного поля геометрическими образами являются векторные линии – такие линии, в каждой точке которых в данный момент времени касательная совпадает с направлением вектора поля.

М

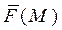
Пусть уравнение векторной линии имеет вид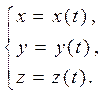

Тогда из условия коллинеарности вектора касательной 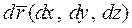и поля 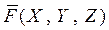получаем систему дифференциальных уравнений для определения векторных линий

.

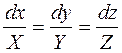Пример 1. Найти уравнение векторных линий поля скоростей, вращающегося тела с постоянной угловой скоростью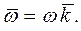

В этом случае

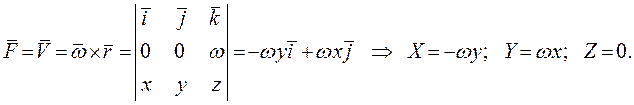
Тогда 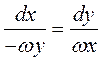или 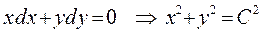- множество концентрических окружностей,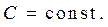

6.2. Формула Гаусса - Остроградского

Теорема 1. Если функции являются непрерывными функциями вместе со своими частными производными первого порядка, то имеет место формула

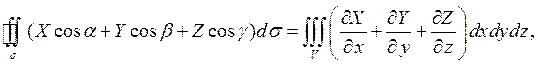(1)

где - направляющие косинусы единичного нормального вектора 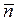к поверхности , которая является границей области V.

Замечание 1. Нетрудно заметить, что 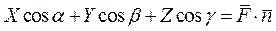и тогда поток векторного поля 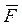определяется по формуле

.

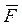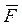Пусть задано векторное поле . Рассмотрим некоторую точку М и окружим её поверхностью . Вычислим поток через эту поверхность. Если 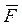- поле скоростей текущей жидкости, то возможны следующие случаи:

1. 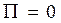- количество втекающей жидкости равно количеству вытека-ющей жидкости;

2. 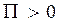- количество втекающей жидкости меньше вытекающей;

3. 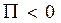- количество втекающей жидкости больше вытекающей.

Во втором случае точка M называется источником, в третьем – стоком.

Рассмотрим отношение

,

где V - объём области с границей . Это отношение представляет собой среднюю мощность источников или стоков, находящихся внутри области V.

Определение 2.Дивергенцией векторного поля 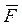в точке М назы-вается

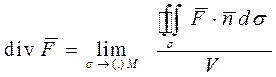. (2)

Таким образом, дивергенция в точке представляет собой мощность источника или стока, находящегося в этой точке.

Формулу (2) с учетом формулы (1) можно преобразовать к виду

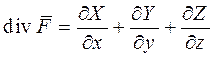. (3)

Замечание 2. В обозначении дивергенции формула (1) представляется в векторной форме

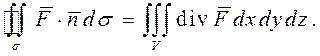
Определение 3. Если в каждой точке векторного поля выполняется условие

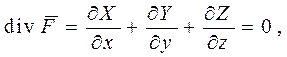
то такое поле называется соленоидальным.

Это поле, которое не имеет источников и стоков. Так, например, в рассмотренном выше примере поле

является соленоидальным.

6.3. Формула Стокса

Теорема 2. Если функции 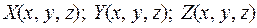являются непрерывными функциями вместе со своими частными производными первого порядка, то имеет место формула

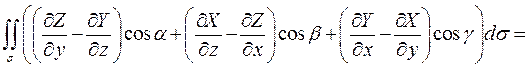
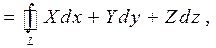(4)

где L - граница поверхности .

Определение 4. Вектор

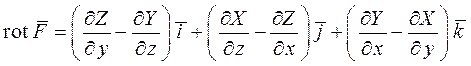
называется вихрем или ротором векторного поля .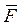

Если 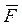поле скоростей текущей жидкости, то можно показать, что равен удвоенной угловой скорости вращения бесконечно малой частицы в точке М, т.е. ротор характеризует вращательную способность векторного поля.

Замечание 3. В обозначении ротора формула (4) представляется в векторной форме

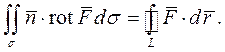
Определение 5. Значение интеграла

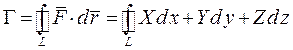
называется циркуляцией векторного поля 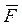вдоль контура L.

Аналогично, как и для плоского случая можно показать, что условие независимости криволинейного интеграла от пути интегрирования сводится к выполнению соотношения

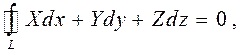(5)

где L - произвольный контур.

С учётом формулы Стокса условие (5) принимает вид

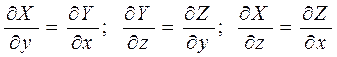, (6)

т.е. .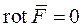

Это означает, что выражение 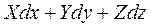является полным дифференциалом, т.е. существует такая функция 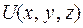, для которой выполняется 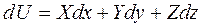, где

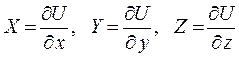
и

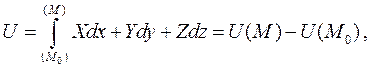
где 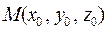- фиксированная точка, - текущая точка, а путь интегрирования выбирается произвольно.

Определение 6. Векторное поле, для которого выполняется условие 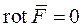, называется потенциальным или безвихревым, а сама функция 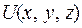потенциалом.

Пример 2. Показать, что поле 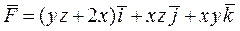является потенциальным и найти его потенциал.

Проверим выполнение условий (6):

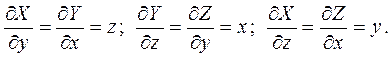
В качестве пути интегрирования выберем ломаную, звенья которой параллельны координатным осям, как показано на рисунке.

z

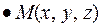
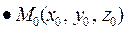
y

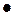
x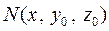

Тогда

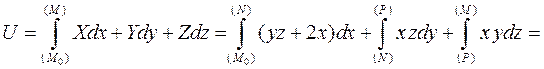
где .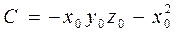

Дата добавления: 2014-11-16